VHDL-AMS Hardware Description Language:VHDL Analog Constructs

VHDL Analog Constructs

VHDL-AMS supports various energy domains implemented by corresponding packages. The common energy domains presently supported by VHDL-AMS-related packages are Electrical, Mechanical, Thermal, and Fluidic [1]. An AMS description for analog electronic circuits begins with the speciﬁcation of the

energy domain of such circuits using the following statements:

library IEEE; use IEEE.electrical_systems.all;

The electrical-systems package enables deﬁnition and declaration of domains, analog ports, quantities, and behavior of analog parts using constructs that are described below.

Natures

In VHDL-AMS the domain used in a description is speciﬁed by the nature construct. A nature construct has two ﬂoating-point aspects: across and through. These aspects are used to model force and ﬂow of the related domain, respectively. In addition, a nature may represent a reference terminal with respect to which the quantity represented by the across aspect is introduced. For example, the across type, through type and reference terminal of the electrical nature are voltage, current, and ground, respectively. Figure 91.1 shows the deﬁnition of the electrical nature.

Natures can be scalar or composite. A composite nature is either an array or record of natures with the same base nature.

Terminals

An analog interface or internal node is referred to as a terminal. Terminals are of the nature type. Figure 91.2 shows two examples of terminal declaration.

Quantities

Quantities are used to represent continuous values in VHDL-AMS. This standard supports three types of quantities: free, branch, and source.

Free quantities, either scalar or composite, represent analog values. Branch quantities are analog values used to model the across or through aspects of terminals, and source quantities are used for response and noise modeling of small-signal spectral in the frequency domain [2].

In an electrical system, across and through branch quantities represent the voltage and current ﬂow between the terminals of the speciﬁed branch.

A branch is declared by its two endpoint terminals. If a branch is between a speciﬁed terminal and the reference terminal it can be represented by its single speciﬁed terminal, i.e., mentioning the reference terminal is not required in its declaration. Figure 91.2 shows the VHDL-AMS model of a nonlinear resistor. The energy domain of this description is electrical_systems. Terminals of this nonlinear resistor are t1 and t2 with electrical nature type. Branch quantities VR and IR are used to model across and through aspects of terminals t1 and t2. The rest of the code shown in this ﬁgure deﬁnes VR in terms of IR.

Attributes

VHDL_AMS includes a number of predeﬁned attributes for terminals, quantities, and signals. As in VHDL, attribute names begin with a single quote (').

'reference and 'contribution are terminal attributes by use of which across and through quantities between the speciﬁed terminal and the reference are deﬁned.

'tolerance, 'above, 'delayed, 'dot, 'integ, 'slew, 'ztf, 'ltf, and 'zoh are predeﬁned quantity attributes in VHDL-AMS. These attributes are discussed below.

• Q'tolerance. Q'tolerance string is used to represent the precision of the scalar quantity Q. VHDL- AMS also allows the designers to deﬁne tolerance groups whose elements are quantities with the same tolerance string. In Figure 91.2, “default_voltage” is deﬁned as the tolerance of VR.

• Q'delayed (T ). This quantity is a copy of quantity Q delayed by time T.

• Q'dot. Q'dot quantity speciﬁes the derivative of quantity Q with respect to time.

• Q'integ. Q'integ quantity speciﬁes the integral of quantity Q with respect to time.

• Q'slew (max_rising_slope, max_falling_slope). This quantity follows quantity Q, but with limited rising and falling slopes.

• Q'above (E ). Q'above is a boolean signal that is true when the value of quantity Q is greater than that of expression E.

• Q'ztf (num, den, t, initial_delay). This quantity represents the z-domain transfer function of quantity Q.

• Q'ltf (num, den). This quantity represents the Laplace-domain transfer function of quantity Q.

• Q'zoh. Q'zoh quantity is the sampled version of the quantity Q.

The 'ramp and 'slew are signal attributes and are used in mixed-signal modeling. S'ramp (t_rise, t_fall) is a quantity that follows signal S with a speciﬁed rise/fall time. S'slew (rising_slope, falling_slope) quantity follows signal S with a speciﬁed slope.

Simultaneous Statements

Simultaneous statements are used for analog modeling. Using simultaneous statements, the behavior of an analog system can be modeled by a set of Differential and Algebraic Equations (DAEs). The left- and right-hand sides of each DAE equation are both either scalar ﬂoating-point-valued expressions or composite expressions with ﬂoating-point subelements. The expressions include any number of (including 0) quantities, constants, literals, signals, and function calls. A simultaneous statement always includes at least one quantity.

For solvability of the DAE equations, the number of equations and unknowns of the equation set must be equal, i.e., the number of simultaneous statements in an architecture must be equal to the sum of the number of free, through, and output interface quantities minus the number of quantities related to output quantities of the instantiated components in the architecture. Simultaneous statements can be used anywhere concurrent statements are allowed [2].

Figure 91.3 models the behavior of a time-variant resister using two simple simultaneous statements. In this model R is a free quantity, while VR and IR are branch quantities. Since this model includes one free and one through quantity, to make it solvable, its behavior is described using two simultaneous equations. The NOW function in this model represents the current time.

Figure 91.4 models the behavior of a capacitor with one DAE. This DAE includes the 'dot attribute to show the direct relation of the capacitor current with the derivative of its voltage.

Simultaneous if and case statements are two other types of conditional simultaneous statements used for modeling the behavior of an analog design. These statements use keywords use and end use for bracketing their statements [4]. Figure 91.5(a) models a clipper using simultaneous if statements. In this circuit the lower and upper bounds of the output voltage are represented by Vmin and Vmax , respectively. The transfer function diagram of this circuit is shown in Figure 91.5(b). The break statement used in this model is discussed in the following sections. The terminal electrical_ref is for the ground terminal.

Another type of simultaneous statements is the procedural statement. This construct allows us to describe the behavior of an analog design using sequential statements enclosed in the pair of procedural and end procedural keywords. A procedural statement may be identiﬁed with a label.

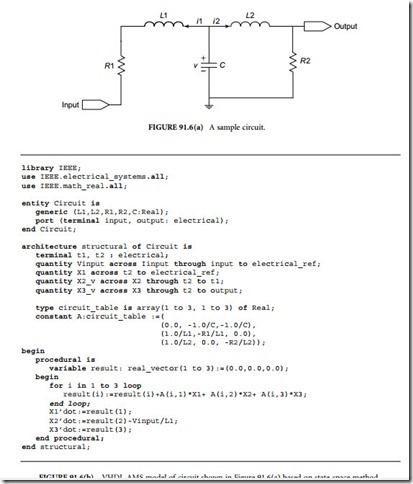
As with other simultaneous statements, a procedural statement appears where a concurrent statement is allowed. This construct may include any sequential statement except wait, signal assignment, and break [1]. Figure 91.6(a) shows an example circuit and Figure 91.6(b) represents the circuit model using state-space method. In this model the state variables (X1, X 2, and X3) correspond to the voltage of C capacitor, the current of L1 inductor, and the current of L2 inductor, respectively. This example illustrates the use of procedural statements. As shown, a procedural statement is similar to VHDL process, and allows use of

variable declarations, sequential constructs (i.e., loop in this example), and variable assignments.

Break Statements

Break statements are used to model the discontinuity in analog models, including discontinuity at the start time which is initialization. When a discontinuity occurs, the analog solver must be informed of the occurred discontinuity and solve the DAEs with new initial values. For an example see the last part of Figure 91.5(a).

Break statements can be categorized into two different types: concurrent break statements, and sequential break statements. Both forms can be used in a conditional clause. Concurrent break statements

appear anywhere a concurrent statement can be used, while sequential break statements appear within a process that is sensitive to the signal or conditions that cause the discontinuity [4].

Break statements may include one or more quantity assignment constructs. In this case, the current value of the speciﬁed quantity is replaced by the value of the represented expression whenever the break statement is executed. Figure 91.7 models an inductor with an initial current. In the body of this description, the inductor current (IL) is set to the integral of its voltage (VL) over its inductance. The break statement shown sets the initial value of IL to 2.0.

Figure 91.8 is the schematic of another example for the description of which we will use the break statement. The code for this example is shown in Figure 91.9. As shown in Figure 91.8, the circuit is composed of an inductor, a resistor, and a switch. The switch position can be altered between A (modeled by Switch=‘1’ )and B (modeled by Switch=‘0’ ) positions. The behavior of this circuit is modeled in Figure. 91.9.

The break statement shown makes the architecture of Circuit sensitive to the Switch input. Occurring an event on Switch input results in describing the behavior of Circuit with the following equation provided that Switch value is 0.

This DAE replaces the original DAE (IL'dot ==IL*(-R)IL+Esource/L) given that Switch value is 0.

Another form of break is the break for statement. This statement is used for initializing quantities that are not directly in the integral form. A quantity is in the integral form if it is an integral quantity or if its 'dot quantity appears in the analog expressions (e.g., IL in example of Figure 91.9). To show the discontinuity of a quantity for which its integral form does not exist, the break for statement is used and indicate which implicit equation must be replaced when the break statement is executed. The selector quantity is represented by a for use clause. Consider Figure 91.10 as an example for this situation. The

DAE of this model does not include the derivative of IL. Thus to indicate which implicit equation must be replaced when a discontinuity occurs on IL, the break for statement is used. In this example IL=>IL'dot*(-L)/R equation replaces the Flux'dot=0 implicit equation when a discontinuity occurs on IL. A break statement can also be used in sequential statements. As discussed above, break on causes sensitivity to signals that appear after the on keyword. Furthermore, for a break without the on part, the condition part of the break statement uses signals of the condition in an implicit break on. Alternatively, in a sequential body, a wait on statement can cause the desired sensitivity. The example of Figure 91.11 uses this alternative. The process statement shown here waits for an event on Switch.

When this occurs, the next statement describes the behavior of the circuit when Switch=‘0’ condition holds. This example is equivalent to code shown in Figure 91.9.

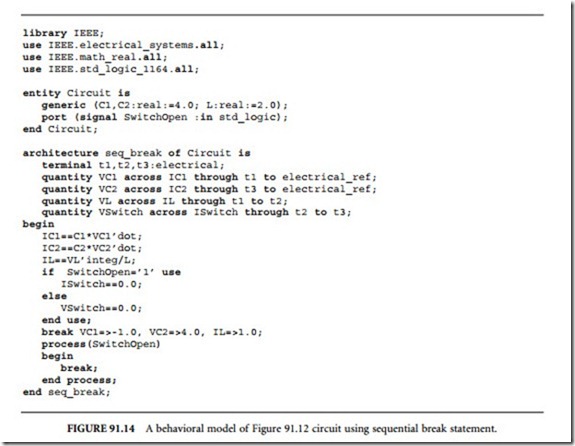
Figure 91.12 is the schematic of another circuit for the description of which we will use the break statement. This circuit is composed of two capacitors; one inductor and a switch. Let us assume that the switch shown has been off before time 0 and switch to on position at time 0. The switch can be in different positions afterwards. Figure 91.13 uses break on statement to model the behavior of this circuit. In this circuit the initial values for C 1 and C2 capacitor voltages and L inductor current are -1.0, 4.0 V, and 1.0 A, respectively. Figure 91.14 models the behavior of the circuit shown in Figure 91.12 using sequential break statement.

Search This Blog

Integrated circuit course