Multidimensional Logarithmic Number System:Binary to Two-Digit 2DLNS

Binary to Two-Digit 2DLNS

From Eq. (84.21), we obtain the two-digit 2DLNS representation shown in the following equation:

Conversion from a two-digit 2DLNS-to-binary is a fairly simple process. Both 2DLNS digits are converted separately using the single-digit method and their results accumulated to produce the final binary representation. There is only one binary representation of the result as binary is a positional number system.

The binary to two-digit 2DLNS process is more difficult as there can be many MDLNS representations for a single number. In Ref. [14], simple LUT tables were used to convert a binary 2’s complement input into a MDLNS representation. The tables were generated by computing all possible MDLNS representations given the full range of B and R and selecting the nearest integer values. This method is clearly not feasible for a real-time hardware solution. There are four known methods for binary to two-digit 2DLNS conversion [29]:

1. The Quick method chooses the nearest first-digit to the target and generates the second-digit to reduce the error, a simple greedy algorithm.

2. The High/Low method chooses the two nearest approximations to the target as the first-digits, generates two associated second-digits for the error and selects the combination with the smaller error.

3. The Brute-Force method operates by selecting the combination with the smallest error, but it uses all possible mantissas of D b as the first-digits instead of just one (Quick) or two (High/Low).

4. The Extended-Brute-Force method improves upon the Brute-Force method by using first-digit approximations above 2.0 and below 1.0 (shifted left or right L bits).

Each method ranges from simple implementations and fairly accurate approximations to difficult implementations and very accurate approximations. The Brute-Force methods, although realizable, require significant hardware resources that may not be worth the gain in accuracy. In some cases it may be more feasible to increase R and use either the Quick or High/Low methods. Therefore, only these two methods will be detailed here; however, more information on the Brute Force methods can be found in Ref. [29].

Quick Method

A two-digit approximation provides many different possibilities to represent a real number in 2DLNS. The only technique found to obtain the best two-digit approximation is an exhaustive search, but a very good approximation can be found using the following simple greedy algorithm, greedy in the sense that it takes as much of the value as possible when selecting the first digit. This method of binary-to-two- digit 2DLNS conversion is referred to as the Quick method as it uses minimal resources and is fast. The algorithm is shown below:

To determine the error for the second-digit approximation, we see that the RALUT output for the first-digit approximation must also include the matched mantissa (see Table 84.7). The size of the RALUT is therefore increased owing to this extra output, but it is a linear, not exponential growth.

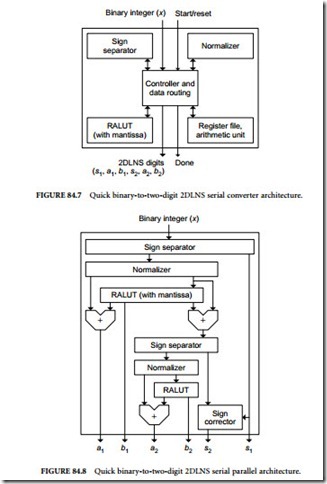
Quick Method Architecture

For the second-digit approximation, the mantissa output of the RALUT is not required. In a serial hardware implementation of this converter, only a single RALUT (with mantissa output) is needed. The first-digit approximation uses the mantissa output while the second-digit approximation ignores it, as in Figure 84.7.

A pipelined hardware implementation of this converter can take advantage of this architecture by using two separate RALUTs (one with the mantissa output and one without) to minimize the area, as in Figure 84.8.

High/Low Method

Although the quick binary-to-two-digit 2DLNS conversion method operates efficiently, it does not always provide the most accurate result. Depending on the choice of R, there can be many possible representations for a given number. The Quick method selects the first digit to be above or below the target value, based on the nearest approximation, but independently of the selection of the second digit.

An alternative method, the High/Low method, generates two representations, one with the first digit below the target and the other with the first digit above the target. In either case, the choice of the two first digits are the two nearest approximations to the target; a modified greedy algorithm. The second digit is generated based on the error calculated from the first digits and the mantissas in the RALUT. The final representation is selected based on the minimum error. To do this, the second RALUT also requires the mantissa output (unlike the Quick method) to generate the final error. Note that one of these final representations will be the same as that produced by the Quick method. This technique is shown in the algorithm below:

Modifying the RALUT for the High/Low Approximation

To implement the High/Low method, the RALUT has to store both the high and low approximations for the first digit. The RALUT addresses are modified to include the range from the low to the high value of each row. The RALUT contents for D = 3, R = 3, and C = 10 are shown in Table 84.8. Note that the high contents of each row are equal to the low contents of the next row. The number of table rows is 2R, one row less than the previous tables, since cyclical connectivity is maintained by using the high element of the last row instead of requiring a new row.

High/Low Method Architecture

For a pipelined hardware implementation, a single RALUT with dual outputs (as in Table 84.8) and two RALUTs with mantissa outputs are needed (see Figure 84.9). For a serial hardware implementation, it is possible to use only one RALUT (dual outputs). The input mantissa can be compared with the two output mantissas to determine the nearest approximation for the second digit. The implementation is similar to that of the quick method (see Figure 84.7) with some additional resources (storage and arithmetic).