SCHEMATIC FUNDAMENTALS:REVIEW OF FUNDAMENTAL ELECTRICAL LAWS

REVIEW OF FUNDAMENTAL ELECTRICAL LAWS

IC layout design is fundamentally the art of implementing an electrical circuit in terms of polygons and shapes, which represent transistors and connections to form the final design. The important concept that we must not forget is that the final design will have electrical characteristics that are very much defined by the characteristics of the physical layout.

The intent of this section is to review a few basic electrical laws and principles that should be understood, so we can establish a good foundation upon which we can move forward and develop efficient and effective layout methodologies.

Ohm’s Law

This is the most basic and fundamental law:

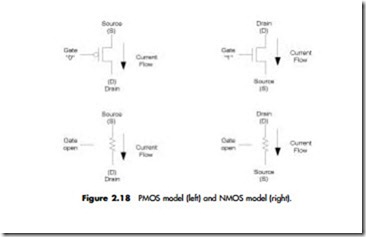
We have seen that MOS transistors operate as “resistors” when they are “on” or when the gate is “open.” The current flow induced by the opening of the gate creates a voltage swing across the transistor. This demonstrates the application of Ohm’s law! Given the resistance of the transistor and a positive current value, the resulting voltage change is explained by Ohm’s law (Figure 2.18).

Similarly, when the gate is “off” the current is “0.” By Ohm’s law, the voltage change is also “0,” which makes sense since the gate is “closed” and it acts like an open circuit.

In reality, the resistance of the transistor is dynamic, as is the amount of current flowing through the transistor. Therefore, this is a very simplistic model,

but it effectively explains how Ohm’s law works and gives us the concepts behind how a transistor operates.

Ohm’s law is a powerful principle to remember and is the foundation for circuit and layout design alike.

Kirchoff’s Current Law

Kirchoff’s current law is another fundamental law that helps us to explain certain concepts in future chapters. Kirchoff’s current law states that the sum of currents into any electrical node is to zero. In this case currents coming into a node are deemed to be positive currents by convention, and currents passing out of a node are deemed to be negative currents, so their overall sum should equal zero:

Another way of stating the same thing is that the sum of currents into a node must equal the sum of currents out of a node (Figure 2.19).

Resistance

We have already mentioned the concept of resistance without really explaining it in more detail. We have used the resistor to model the transistor in the “on” state.

In simple terms resistance can be thought of as the inability (or ability) of a conductor to conduct charge. Using a water analogy, a pipe of large diameter has a lower resistance than a smaller diameter pipe because it can pass a larger amount of water. The cross-sectional area of the pipe is larger in this case. This assumes that the two pipes are the same lengths. As a pipe or conductor increases in length, the resistance also increases.

The convention in IC design for resistance calculation is to characterize each conductor layer in terms of resistance per “square.” One “square” is defined as the condition when the length of the conductor equals the width.

The formula for calculating the resistance of a conductor is

where “r” is the resistivity of the layer measured in W/D, l is the length, and w is the width of the conductor.

Capacitance

In simple terms, capacitance can be thought of as the amount of charge a body or conductor can hold per unit of voltage between the node in question and another reference node. Using our water analogy, a capacitor should be thought of as a dammed lake that is filled with or emptied of water based on the electrical power needs of consumers.

The amount of capacitance a conductor has is determined by the area of the conductor and how far it is away from the reference node. Again using our water analogy, let’s consider a lake. How much water will it take to fill the lake (think how much charge will it take to charge up the capacitor)? The answer is, it depends on the surface area of the lake and how deep it is.

The tricky part of this concept is that the distance between the reference node, the bottom of the lake, and the surface of the lake determines the depth of the lake. The farther the reference node is away from the conductor, the shallower the lake is. If the reference node is very close, the lake will be deeper and thus the overall capacitance is greater. The concept behind this is that the charge in the conductor is attracted to the reference node by an electric field attraction associated with opposite charges. Closer bodies have larger electric fields and thus larger capacitance values.

There is also a dependency on the material that separates the two nodes. Some materials isolate the attraction to a better degree than others do.

A very simple model for the capacitance of a conductor is calculated as

where A is the surface area of the specific conductor, d is the physical distance between the conductor and the reference node, and e is a constant representing the characteristics of the insulating layer between the conductor and the reference node.

Delay Calculation

Without going into gory theoretical detail, let us consider a simple example of a inverter driving a wire or conductor. The wire is represented as a single resistor and a lumped capacitance (Figure 2.20).

Our goal is to calculate the delay from IN to node A. The total delay is dependent on two factors:

• The associated switching delay of the inverter. This inverter delay is dependent on the size of the resistor and the capacitor. This delay is normally calculated or measured from simulation, so we will not consider it formally here.

• The delay of the wire is due to the resistor and the capacitor. A first- order approximation of the delay through the wire as an independent component is

This simple equation gives us an easy formula to analyze the delay through different wiring scenarios and allows us to make the appropriate trade-offs in laying out the final design.

If it is required to minimize the delay through a given circuit, we need to consider reducing both the resistance and the capacitance of the wire. Using our knowledge of resistance and capacitance, we can optimize our layout to minimize the delay by doing the following:

• Minimizing the length of the conductor. This reduces both the resistance and capacitance terms.

• Optimizing the width of the conductor. Decreasing the width of the conductor decreases the capacitance of the wire; however it increases the resistance!

• Increasing the spacing of the conductor to other reference nodes. This decreases the capacitance of the wire. Usually this means running the wire in areas that are free from other polygons or shapes or using a top metal layer instead of the lower one.