Verification Languages:Computation Temporal Logic

Computation Temporal Logic

In this section, theory and practice of model checking and related topics are ﬁrst introduced and then CTL and its application in speciﬁcation of properties will be described.

Formal Verification

The need for reliable hardware systems is an important issue and the involvement of these systems in our daily life is increasing day by day. The rapid growth of technology inquires into the methods that increase our conﬁdence in the correctness of these systems. To increase the level of this conﬁdence, we highly need robust techniques to verify these systems. Simulation is the traditional approach for verifying ﬁnite-state systems, but its problems are: working much slower than the real system, being expensive and having no guarantee for all possible input combinations to be simulated. For these reasons, the application of formal veriﬁcation (FV) is increasing every day. Formal veriﬁcation is the process of checking whether a design satisﬁes for requirements (properties) speciﬁed in a logical language or not.

Formal veriﬁcation is a new emerging hardware validation method. It is an alternative to simulation in some designs, and complementary to simulation in many others. Different formal veriﬁcation methods have been proposed that make it useful for hardware veriﬁcation. Among these methods model checking is mostly used which is described in the next subsection.

Model Checking

Model checking [1,2,3] is the most popular formal veriﬁcation technology for property veriﬁcation. In this method, the veriﬁcation problem is reduced to graph algorithmic problems that can be fully auto- mated. This method, which is relatively easy to use, generates a counterexample if the property is not satisﬁed. A counterexample describes conditions in the design under which a property cannot be satisﬁed. Model checking uses transition systems (Kripke structure) to model systems [1,3] and temporal logics to specify properties. To understand the term “model,” we need to be familiar with transition systems and Kripke structures which are described as follows.

Transition System

A transition system [1,3] is a structure TS = (S, S0, R), where S is a ﬁnite set of states, S0 Í S the set of initial states, and R Í S ´ S a transition relation that should be total, i.e., for every s in S there exists s¢ in S such that (s, s¢) is in R("s ÎS $ s¢ ÎS,(s,s¢) ÎR).

Kripke Structure

A Kripke structure [1,3] models a system deﬁned by M = (S, S0, R, AP, L). In this structure, (S, S0, R) is a transition system. An atomic proposition directly corresponds to a variable in the design being veriﬁed. AP is a ﬁnite set of atomic propositions. L is a labeling function that labels each state with a set of atomic propositions that are true in that state. Together, atomic propositions and L convert a transition system into a model.

A computation [3] in a model, as shown in Figure 92.1, is the basic object of reasoning. A complete computation consists of several time frame each expressed in a path or a tree. Linear time logic (LTL) expresses a computation in a path, while CTL is used for a computation tree with branches. In linear time we use LTL and consider individual computations starting from s0 (the ﬁrst state). In contrast, in branching time we look at a computation tree (CTL) originating from s0.

As mentioned before, two main aspects of model checking are model representation and property speciﬁcation. Models are represented by Kripke structures which are described here. For property spec- iﬁcation we used temporal logics described later.

Temporal Logics

Properties are characteristics of a design that should hold if the design is to perform certain functions. For example, a property of a 4-bit BCD counter that rolls over is that the next count after 9 is always 0. The foremost step to verify a system is to specify the properties that the system should have. For example, if we want to prove that a system never deadlocks, we have to specify a set of properties for that system. These properties are represented by temporal logic. Temporal logic refers to representation of time-dependent information within a logical framework.

CTL is a version of temporal logic which is currently one of the popular frameworks used in verifying properties of concurrent systems.

In this section, we focus on temporal logic for model checking. Once we are familiar with the important properties, the second step is to construct a formal model for the system being veriﬁed. The model should capture properties that must be considered for the establishment of correctness of a system. Model checking includes traversing the state transition graph (Kripke structure) and verifying whether it satisﬁes the formula representing the property or not; or more concisely, whether the system is a model of the property or not.

CTL Model-Checking Steps

A CTL formula [3] in a given state of a Kripke structure is either true or false. Its truth is evaluated from the truth of its subformulas in a recursive fashion, until atomic propositions (variables of system being veriﬁed) which are either true or false in a given state, are reached. A formula is satisﬁed by a system if it is true for all the initial states of the system.

Mathematically, suppose a Kripke structure K = (S, S0, R, AP, L) (system model) and a CTL formula Y (speciﬁcation of the property) are given. We have to determine if K ú = Y is satisﬁed; this expression reads as K is a model of Y. It holds if K ú = Y holds for every initial state, s 0, of K in the set of S 0 states, i.e., K , s0ú = Y for every s0 ÎS0. If the property does not hold, the model checker will produce a counterexample, which is an execution path that cannot satisfy the speciﬁed formula (Figure 92.2).

CTL Formulas

Atomic propositions, standard Boolean connectives of propositional logic (e.g., AND, OR, NOT), and temporal operators are used all together to build CTL formulas.

A temporal operator is composed of two parts, a path quantiﬁer (universal (A) or existential (E)) followed by a temporal modality (F, G, X, U), which are described in the next subsections. A CTL property is interpreted relative to an implicit “current state”. There are generally many execution paths (sequences) of state transitions of a system starting from the current state.

A path is an inﬁnite sequence of states (s 0, s1, s2 , …) for (si , si+1) E R to hold for all i. Consider the modulo-8 counter shown in Figure 92.3, variables of system in this example are v0, v1, and v2. The domain of these variables is {0, 1}, which means that these variables can hold either 0 or 1. As mentioned above, a state is a function that assigns a value to each variable in its domain. For example, if s(v 0) = 0, s(v1) = 1, and s(v2) = 1, the state is (1 1 0).

Since a set of states can be selected by a formula, we can predicate states using this state diagram. For example, X = v2 Ú v 0 selects the set {100, 101, 110, 111, 001, 011}. Similar to states, since a set of transitions can also be selected by a formula, we can predicate the transition relation as well. For example, consider function R3 = (v2 ¹ v2¢) where v2 and v2¢ are the values before and after a transition respectively. As shown in Figure 92.3, the only transitions in which v 2 in one state is not equal to v2 of the next state are t 0 and t1, therefore R3 = {t 0, t1}.

Path Quantifiers

The path quantiﬁer indicates if the modality, which deﬁnes a property, is true for all the possible paths or the property only holds on a few paths. The former case is denoted by the universal path quantiﬁer, A, while the latter case is denoted by the existential quantiﬁer, E. Properties that begin with A are called ACTL and those beginning with E are called ECTL.

Temporal Operators

The temporal modalities describe the ordering of events in time in an execution path. They can be F, G, X, and U described below.

• F Æ (which is read as “ ‘Æ’ holds sometime in the future”) is true in a path if there exists a state in that path where formula ‘Æ’ is true.

• G Æ (which is read as “ ‘Æ’ holds globally”) is true in a path if ‘Æ’ is true at every state in that path.

• X Æ (which is read as “ ‘Æ’ holds in the next state”) is true in a path if ‘Æ’ is true in the state reached immediately after the current state in that path.

• Æ U j (which is read as “ ‘Æ’ holds until ‘j’ holds”) is true in a path if ‘j’ is true in a state in that

path, and ‘Æ’ holds in all preceding states of that state.

CTL Syntax

The general syntax of CTL expressions including variable names, indexing, formulas, and combination of formulas are described below. Examples provided later in this chapter show utilization of these structures.

• TRUE, FALSE, and var-name == value are CTL formulas, where var-name is the name of a variable, and value is a legal value in the domain of that variable.

• var-name1 == var-name2 is the atomic formula that is true if var-name1 has the same value as var-name2. var-name1[i:j] == var-name2[k:l] can be used if the lengths of vectors are equal. These characters may be used for variable names and values: A–Z a–z 0–9 ^ ? | / [ ] + *

$ < > ~ @ _ # % : " '.

• If f and g are CTL formulas, the following combinations are also considered as formulas. In these formulas, symbols of Table 92.1 are used.

• (f ), f Ù g, f Ú g,f Ù g, !f , f ® g, f ¬® g,

• AG f, AF f, AX f, EG f, EF f, EX f, A(f U g) and E(f U g).

In the above, AX:n(f) is allowed as a shorthand for AX(AX(. . . AX(f). . . )), where n is the number of invocations of AX. Also, the term EX:n(f) is deﬁned similarly. The operators used in the formulas and shown in Table 92.1 have the precedence shown in Table 92.2. A complete formula, the elements of which are shown above, should be followed by a semicolon. Text written from # to the end of a line is considered as a comment.

CTL Semantics

A brief overview of the semantics of CTL is given below. In this overview K is considered as a Kripke structure and s a typical state of this structure. The semantics of the CTL operators are stated below:

• K ,sú = EX(Y): There exists s¢ such that s ® s¢ (R(s, s¢)) and K, s¢÷ = Y. It means that s has a successor state s¢ at which Y holds.

• K ,sú = EU(Y1, Y2) iff there exists a path L = s0, s1, … from s and k >= 0 such that K, L(sk)÷ = Y2, and if 0 £ j < k, then K, L(sj)÷ = Y1. It means that Y1 should hold in all states of a path until we reach to a state in which Y2 is satisﬁed.

• K ,sú = AU(Y1, Y2) iff for every path L = s0, s1, … from s there exists k >= 0 such that K, L(sk)÷ = Y2, and if 0 £ j < k, then K, L(sj)÷ = Y1. It means that for all paths Y1 should hold in all states until we reach to a state in which Y2 is satisﬁed.

• AX (Y): There is no case where a next state exists at which Y does not hold, i.e., for every next state Y holds.

• EF (Y): There exists a path L from s and k>= 0 such that K, L (sk)÷ = Y.

• AG (Y): There is no case where a path L from s exists and k>= 0 such that K, L(sk)÷ = Y, i.e., for

every path L from s and every k >= 0; K, L(sk )÷ = Y.

• AF(Y): For every path L from s, there exists k>= 0 such that K, L(sk)÷ = Y.

• EG(Y): There is no case where for every path L from s there is a k >= 0 such that K, L(sk)÷ = Y.

It means that there exists a path L from s such that, for every k>= 0: K, L(sk )÷ = Y. In other words,

there is path in which all states satisfy Y.

To clarify the concept, several basic CTL operators stated above are shown graphically in Figure 92.4 to clarify the concept. In this ﬁgure, states that satisfy the property are marked using Ö and states that do not satisfy the property are marked using ´.

CTL Formula Conversions

After property speciﬁcation and model representation, we should verify the model against each of its properties that are described in CTL. For this purpose, a CTL formula should be checked against the states of the model being veriﬁed. For a universal CTL formula (ACTL), all states in a design that are reachable from the initial states should be checked. However, for an existential CTL formula (ECTL), only one case from the initial states should be found that satisﬁes the formula. It is clear that algorithms of existential CTL formula can be implemented easier than that of universal CTL formula.

Universal formulas can be converted into existential formulas. That is, all universal path quantiﬁers can be replaced with the appropriate combination of existential quantiﬁers and Boolean negations. “ﬁnally” (F) operators are also converted into “until ” (U) operators. This returns a new formula that may look different from the original one (even the strings are different), but has the same semantics. These conversions are shown in Table 92.3.

Building a Computational Tree

We usually use the CTL, which is a version of temporal logic, for specifying formulas for model checking. But usually, design representations are not in tree forms. They are usually in the form of a transition

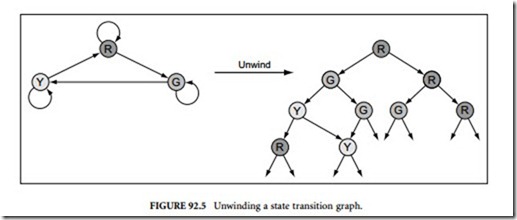
graph called state transition graph (STG). In model checking, a STG is used to derive a computation tree that CTL formulas are applied to. In the following discussion, we show how a tree can be built from a given STG. For this purpose, the graph structure is unwounded into an inﬁnite tree rooted at the initial state.

Figure 92.5 shows an example of unwinding a graph into a tree. The example is a trafﬁc-light controller where R, G, and Y indicate RED, GREEN, and YELLOW, respectively. All possible computations of the system being modeled are represented by the paths in the tree. Formulas in CTL, refer to the computation tree derived from the original graph. Because of its operators that describe the branching structure of the tree, CTL is classiﬁed as a branching time logic.

To illustrate the usage of a tree, we describe several formulas for the tree in Figure 92.5. The formula EG (RED) is true, since there exists at least one path where all of its states are RED (the path R, R, R, …). The formula E (RED U GREEN) is also true since there is at least one path, where all the states hold R until we reach a state with G (R, R, G …). But the formula AF (GREEN) is false, since there is at least one path in which no state has the atomic proposition G.

Specification of Properties in CTL

There exist few CTL formulas that are hard to interpret. Therefore, a designer may fail to understand which property has been actually veriﬁed. In this section, we will add several common constructs of CTL formulas used in hardware veriﬁcation.

• AG (Request ® AF Acknowledgement): For all reachable states (AG), if Request is asserted in the state, then at some later point (AF) we must reach a state where Acknowledgement is asserted. AG is interpreted relative to the initial states of the system, whereas AF is interpreted relative to the state where Request is asserted. A common mistake would be writing Request ® AF Acknowledgement in the AG (Request ® AF Acknowledgement). The meaning of the former is if Request is asserted in the initial state, it is always the case that eventually we reach a state where Acknowledgement is asserted. The latter requires that the condition is true for any reachable state where Request holds. If Request is identically true, AG (Request ® AF Acknowledgement) reduces to Acknowledgement.

• AG (AF DeviceEnabled ): The proposition DeviceEnabled holds indeﬁnitely on every computational path, starting with the starting state.

• AG (EF start): From any reachable state, there must be a path starting from that state which reaches a state where start is asserted. In other words, it must always be possible to reach the start state.

• EF (x Ù EX (x Ù EX x)) ® EF ( y Ù EX EX z): If it is possible for x to be asserted in three consecutive states, then it is also possible to reach a state where y is asserted; and from there to reach a state where z is asserted in two more steps.

• EF (~Ready Ù Started): It is possible to reach a state where Started holds, but Ready does not hold.

• AG (Send ® A (Send U Receive)): It is always the case that if Send occurs, then eventually Receive

is true, and until that time, Send must continue to be true.

• AG (in ® AX AX AX out): Whenever in goes high, out will go high within three clock cycles.

• AG (~storage_coke® AX storage_coke): If the coke storage of a vending machine becomes empty, it is recharged immediately.

• AG AF ((~storage_coke Ú ~storage_coffee) Ù (storage_coke Ù storage_coffee)): The recharge transaction

of a vending machine (of coke and coffee) often takes place indeﬁnitely.

Model-Checking Example: SAYEH Controller

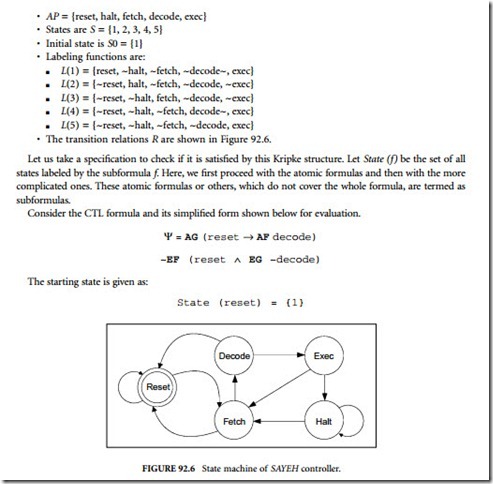
In this section, we illustrate model checking using CTL with a small example that is the controller part of a simple processor called SAYEH. This processor has also been described in Chapter 86. The architecture of this processor is simple, but it has a good number of hardware components for formal veriﬁcation. The SAYEH processor has a 16-bit data bus and a 16-bit address bus. It has 8- and 16-bit instructions. Short instructions may contain shadow instructions, which effectively pack two such instructions into a 16-bit word. The state transition graph of its controller is shown in Figure 92.6.

The controller’s Kripke structure is described below by stating the set of states S, the initial state S0, the atomic proposition AP, the labeling function L and the transition relation R. The details of this structure are:

Our Coverage of CTL and Formal Verification

Formal veriﬁcation replaces simulation in certain applications. For testing the correctness of a digital system that consists of FSMs, formal veriﬁcation is efﬁcient and easy to use. This is an exact method and does not require test data. This section convers the topics related to model checking of hardware systems, focusing on the CTL property language that is used for property speciﬁcation. In addition, we covered basics of developing properties for components of a design. We also presented ways of verifying a typical system. Methods described here are general and are applied to most hardware systems. Another property language used for formal veriﬁcation and assertion veriﬁcation is PSL. This language will be discussed in the next section.

Search This Blog

Integrated circuit course