SCHEMATIC FUNDAMENTALS:LOGIC GATES

LOGIC GATES

The majority of schematics today are not ﬁlled with transistors. The reasons for this are many, but the main ones are that it is impractical because of the complexities of the designs that are undertaken, and that transistors are grouped into what is called a logic gate or “gate.” A logic gate could be confused with the gate of a transistor, but we hope that the context in which the term is used will be sufﬁciently obvious.

Logic gates are implemented directly or in combination to form Boolean logic functions. Theoretically, almost any Boolean logic function can be implemented with a single logic gate, but in practice this is not done. We hope that, after reading this book, you will fully understand why.

In general, most logic functions are implemented in CMOS using inverters, two to four input NANDs, two to four input NORs, and transmission gates. Let’s begin to learn about these gates by understanding the simplest of all logic gates: the inverter.

Inverter

As the name implies, the inverter is the simplest logic gate. Its function is to invert the signal received on the input node to the opposite polarity to the output node (Figure 2.7).

Let’s use our knowledge of transistors. Knowing that the PMOS is “open” when receiving a “0” means that the “1” is driven to the output. In this case the NMOS is off and does not affect the output level. Conversely, by the same rules, a “0” is produced when the input is a “1” (Figure 2.8).

CMOS logic by its very nature is always inverting. Also note that the NMOS and PMOS are never “on” at the same time. This demonstrates the reason why CMOS is a low-power style of circuit design. Once the gate switches state, there is no DC current path between VDD and VSS; such a path, if it existed, would consume DC power.

In specifying the inverter size, now two device sizes are required (Figure 2.9).

• The “P” and “N” identiﬁers specify the device type. Again, generally the widths are stated ﬁrst.

• In this case the PMOS transistor width is 2 mm, and that of the NMOS is 1 mm.

• The PMOS transistor length is 0.5 mm, and since the NMOS is not shown it is assumed to be the default value for the process.

In the next sections NAND and NOR gates will be covered. NANDs are inverted AND gates and NORs inverted ORs. They both are single-stage gates, and this is one reason why they are the basic building blocks of CMOS logic.

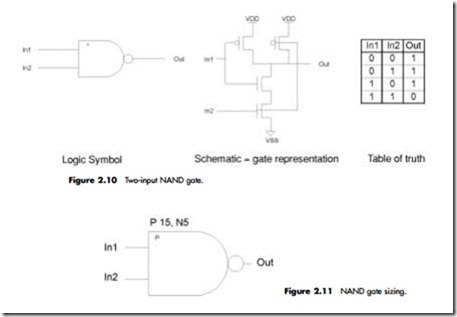
Two-Input NAND Gate

When a logical decision is required to be made between different signals, NAND and NOR gates will do the job. By following the operation of the individual transistors under each input condition in the truth table of Figure 2.10, you will see that the desired output is produced with the transistor conﬁguration shown.

The “Not AND” function (OUT = “0”) is produced when both IN1 and IN2 are both “1.” The requirement for both inputs to be “1” simultaneously is achieved by connecting the two NMOS transistors in series. At the same time, the PMOS transistors are connected in a complementary fashion by being in parallel.

This conﬁguration not only produces the correct functionality from the gate, but also results in eliminating static DC power consumption by ensuring that there is never a condition in which a PMOS path to VDD and an NMOS path to VSS are “on” simultaneously.

Three or more input NAND gates are easily implemented by extending the series connections of the NMOS and the parallel connections of the PMOS transistors.

In specifying the NAND gate transistor sizes, four device sizes are now required. In most cases, however, all PMOS transistors will be the same size and, similarly, all NMOS transistors will be the same size; therefore, once again typically only two values are required (Figure 2.11). This is also true of NOR gates, and indicating sizes on the NOR gate is done in a very similar way.

• The “P” and “N” identiﬁers specify the device type. Again, generally the widths are stated ﬁrst.

• In this case the PMOS transistor width is 15 mm, and 5 mm for the NMOS.

• The PMOS and NMOS transistor are assumed to be the default value for the process.

If distinct sizing for the two separate PMOS transistors is required, typically this would be indicated by a subscript to the “P” identiﬁer such as “P1, P2,” and additional values would be given.

Two-Input NOR Gate

The NOR gate is the mirror or complementary conﬁguration to the NAND. In the NOR gate the series/parallel connections are reversed between the NMOS and PMOS transistors—the PMOS transistors are in series and the NMOS in parallel (Figure 2.12).

Once again, the potential for DC power consumption is eliminated under all input conditions, and three or more input variations of the NOR are easily made by increasing the series and parallel connections of the PMOS and NMOS transistors, respectively.

Transistor size values are indicated in much the same way as for NAND gates, and a description of a typical convention will not be repeated here.

Complex Gates

As mentioned previously, almost any Boolean logic function can be implemented in a single-stage CMOS logic gate. The term complex gates is the name given to logic gates that have a “complex” function, usually a combination of AND, OR, NAND, and NOR, all implemented in one logic stage.

Because complex gates are implemented in a single stage, in almost all cases power consumption, area, and speed beneﬁts are achieved.

Figure 2.13 is an example of a complex logic function implemented in multiple gates.

If we do a simple transistor count for this logic we ﬁnd that there are 16 transistors in all with 3 stages of logic. It is very common to ﬁnd that an engineering schematic would not be designed this way but in a single stage of logic represented by a symbol such as that shown in Figure 2.14.

By combining the inverters with their respective driving gates, you can see that the NAND–inverter combination becomes an AND and the NOR–inverter combination becomes the OR. The output NOR remains the same.

What does the transistor representation of this gate look like? We need this representation to do our layout design.

This type of complex gate is very efﬁcient to use and build, but somehow cumbersome to draw. To determine the transistor representation we analyze the logic starting from the output gate and work backward (i.e., from right to left).

First consider the output of a two-input NOR. The idea is to combine a NAND function representing the AND gate as well as a NOR function representing the OR gate into the output NOR to create the ﬁnal logic gate.

Why do we use an input NAND instead of AND? Similarly, why NOR instead of OR?

The answer is that the output NOR gate provides an extra stage of logic inversion, which we take advantage of in implementing the ﬁnal gate. Since there is an inherent inversion in the output NOR gate, we do not need to implement input AND or OR functions; NAND and NOR functions are just what we need. It is wise to work this through and prove it to yourself.

Before we can perform the transistor merging as described later, the prepa- ration step is to determine the logic gates at the input that will be merged into the output gate. This is done by simply inverting the logic at the inputs. In our case we invert the AND to NAND and the OR to a NOR.

1. We replace the AB PMOS transistors with the parallel PMOS transistors of an input NAND and the AB NMOS transistors with the respective series NMOS transistors of the same input NAND.

2. Now we use the same methodology, but for the CD devices. Replace the CD PMOS transistors with the series PMOS transistors of the input NOR and the CD NMOS transistors with the respective parallel NMOS transistors. There—you’re done! (See Figure 2.15.)

If you check the truth table of the ﬁnal conﬁguration you should ﬁnd that the 8-transistor logic gate is logically equivalent to the 16-transistor, 3-stage logic function presented earlier.

Use this technique to expand and understand the simplicities of complex gates!

Because of the greater number of transistors for a typical complex gate, individual transistor sizes may or may not be indicated on the schematic. In most cases each transistor would have a different size, and so transistor sizes are typically omitted from the symbol. Size information must be determined by looking at the transistor-level schematic. Even if sizes are indicated, the mapping of these sizes to the transistor conﬁguration should be manually checked before layout begins.

Search This Blog

Integrated circuit course