Multidimensional Logarithmic Number System:Applying an Optimal Base to Input Data

By -
Applying an Optimal Base to Input Data

We have seen how applying an optimal base to the coefficients of a digital filter can significantly increase the accuracy of the mapping to 2DLNS. This same improvement can be seen when applied to the input

Multidimensional Logarithmic Number System-0192

data of the filter; however, the nonbinary bases must be the same for both data and coefficients for the 2DLNS arithmetic to operate properly. For implementation efficiency the sum of the corresponding coefficient and input data indices should never overflow while performing a 2DLNS multiplication. We can guarantee that this situation will never happen by limiting the range on both the coefficient and data exponents. For example, with the earlier one-digit optimal base case, the nonbinary exponent range is 9 bits or [-256, 255]. To avoid overflow we could limit the range on the two-digit input data mapping nonbinary exponent from [-32, 31] (or 6 bits), which would require a change to the range of the coefficients to [-224, 224] to prevent overflow on the sum (9 bits only). Changing these limits requires that we recalculate the optimal base, which results in slightly lowering the stop-band attenuation of 77.741 dB from the original value of 80.315 dB. Our range of the input data nonbinary exponent influences the input data mapping. In this case we are unable to achieve a complete error-free mapping. Table 84.12 summarizes the results from three different input ranges for an optimal base selected from the coefficients. Another approach to limit the number of nonerror-free input representations is to find the optimal base for the inputs themselves. Doing this will significantly limit the stop-band attenuation as the coefficients are single digits and mapped using the optimal base from the input data. Table 84.12 also includes results from this approach. Clearly, for the one-digit coefficient/two-digit input data case one has to select what should be prioritized.

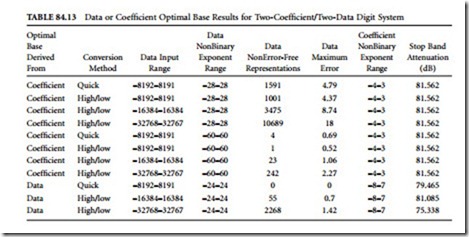
We will explore the same scenario with the two-digit case where the coefficient nonbinary exponent range is [-4, 3]. Since this range is very small, we need only limit the input data nonbinary exponent ranges, initially, to [-28, 28] so that the range of the sum is [-32, 31] (or 6 bits). Our stop-band attenuation does not change from 81.562 dB; however, the data mapping is far from being error-free. Table 84.13 summarizes the results from the same three input ranges as in the previous case. To try to improve the input data mapping, the nonbinary exponent ranges can be increased to [-60, 60] which results in better mapping (see Table 84.13), but larger LUTs in the inner product processor. The alternative, again, is to optimize the base for the input data. In the single-digit case earlier, the stop-band attenuation suffered as a result of the coefficients not being mapped as well as before. To avoid this, we can increase the range on the coefficients to [-8, 7]; therefore, providing more possible representations and reducing

Multidimensional Logarithmic Number System-0193

the input data nonbinary exponent range to [-24, 24] to maintain the same dynamic range at the output of the adder as before. This approach allows a completely error-free mapping for an input range of [–8192, 8191] with a simpler converter, but limits the size of the inner product LUTs. Table 84.13 summarizes the results for other ranges. For two-digit input data and coefficient architectures, this appears to be the best approach for minimizing hardware and computational error.

Multidimensional Logarithmic Number System-0194

Comments

Post a Comment

Popular posts from this blog

Square wave oscillators and Op-amp square wave oscillator.

By -
Image
Square wave oscillators If Fourier analysis is performed on a square wave it is found that the waveform is composed of many harmonics of the fundamental frequency. This rich harmonic content makes the square wave particularly useful as a quick test of amplifier performance. Examples of possible results are shown. The simplest way to produce a square wave is to make a sine wave oscillator in one of the ways described earlier, then feed the output to some form of squaring circuit such as a Schmitt trigger. This is the method adopted in most commercial sine/square wave generators. There are, however, several circuits for square wave oscillators and a description of the most common follows. Multivibrator Technically the multivibrator is a relaxation oscillator, working on the charging of a capacitor through a resistor. If a negative edge is applied to the circuit in (a), transistor TR 1 turns off the for time taken for the base voltage to return to 0 V. If the voltage step is
Read more

Timing Description Languages:SDF

By -
Image
SDF Standard Delay Format (SDF) is an ASCII format used to convey timing information between EDA tools. SDF was first developed by Cadence in 1990. Open Verilog International (OVI) approved SDF version 2 in 1993 and SDF version 2.1 and 3 in the following years. Improving SDF version 3 features, resulted in IEEE Standard 1497 [1]. Role of SDF in Design Process SDF can be used in different levels of a design process to annotate timing specifications, including timing data and constraints. Timing constraints are used during the forward-annotation process while timing data are applied during the back-annotation process. Forward-annotation process deals with porting timing constraints to synthesis, floorplanner, layout, and routing tools to meet the required constraints. During the design process, timing data can be back-annotated to analysis tools (including simulators, static timing analysis tools, etc.) to provide more accurate timing representations. SDF Structure An SDF f
Read more

Adders:Carry Look-Ahead Adder.

By -
Image
Carry Look-Ahead Adder As previously stated, the carry, c i +1, produced at the i -th position is calculated as c i +1 = x i · y i ∨ c i ·( x i ⊕ y i ). This means that a carry is generated if both x i and y i are 1, or an incoming carry is propagated if one of x i and y i is 1 and the other is 0. Therefore, letting g i denote x i y i , we have c i +1 = g i ∨ c i p i , where p i = x i ⊕ y i . Here, g i is the formula for the carry generation condition at the i -th position, i.e., when g i is 1, a carry is generated at this position. Substituting g i –1 ∨ p i –1 c i –1 for c i , we get A carry look-ahead adder can be realized according to this expression, as illustrated in Figure 41.10 for the case of four bits [21]. According to this expression, c i +1’s are calculated at all positions in parallel. It is hard to realize an n -bit carry look-ahead adder precisely according to this expression, unless n is small, because maximum fan-in and fan-out restriction is violated at higher
Read more