Operational Trans conductance Amplifiers:OTAs with High Drive Capability.

OTAs with High Drive Capability

For driving capacitive loads (or small resistors), a large available output current is necessary. In the OTAs shown so far, the amount of output current available is equal to twice the quiescent current (i.e., the tail current I0). In some situations, this current can be too small. There are several ways to increase the available current in an efficient way. To achieve this, four design principles will be discussed here.

1. Increasing the quiescent current by using current mirrors with a current transfer ratio greater than 1.

2. Using a two-transistor level structure to drive the output transistors.

3. Adaptive biasing techniques.

4. Class AB techniques.

OTAs with 1:B Current Mirrors

One way to increase available output current is to increase the transfer ratio of the current mirrors CM1 and CM2 by a factor B, as indicated in Figure 25.7 [4]. The amount of available output current and also the overall transconductance increase by the same factor. Unfortunately, the –3 dB frequency of the CM1–CM2 current mirrors will be reduced by a factor (B + 1)/2 due to the larger gate–source capacitance of the mirror output transistors. Moreover, wT will increase, w2 will decrease, and the ratio w2/wT will be strongly deteriorated. The amount of available output current though is B times the tail current. It is also possible to increase the current transfer ratio of current mirror CM3 instead of CM1. A better current efficiency then results, but at the expense of more asymmetry in the two signal paths. Although the amount of the maximum available output current is B times the tail current in both situations, the ratio between the maximum available current and quiescent current of the output stage remains equal to two, just as in the OTAs discussed previously.

OTA with Improved Output Stage

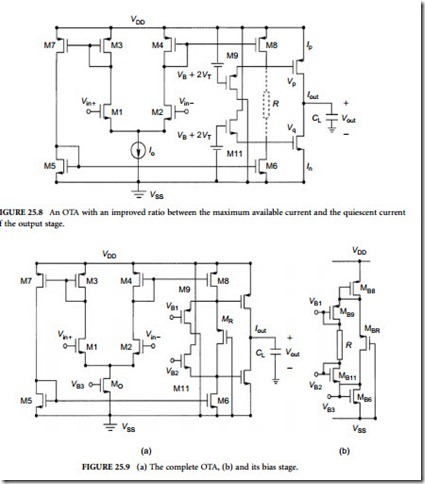
Another way of increasing the maximal available output current is illustrated in Figure 25.8 [5]. It improves upon the factor 2 relationship between quiescent and maximal available current. Assuming equal K factors for all transistors shown in the circuit leads to the conclusion that the effective gate–source voltage of transistor M11 (= VGS11 – VT11) equals that of transistor M1 (= VGS1 – VT1), since they carry the same current, assuming that transistors M1, M4, and M6 are in saturation. Because the current drawn through transistor M9 is equal to the current in transistor M2, their effective source–gate voltages must also be equal assuming equal K factor for M2 and M9. Since the sum of the effective gate–source voltages transistors M11 and M12, and also of M9 and M10, is fixed and equal to VB, a situation exists which is equivalent to the two transistor level structure described in Ref. [6].

The ratio between the maximum available output current and the quiescent current of the output stage can be chosen by the designer. It is equal to (VB/(VB – VGS0))2, where VGS0 is the quiescent gate–source voltage of transistor M11.

If the OTA is used in an overdrive situation Vin> (2I0 ) K , then either M6 or M5 will be cut off,while the other transistor carries its maximum current. As a result, one of the output transistors (M10 or M12) carries its maximum current, while the other transistor is in a low-current standby situation. The maximum current that one of the output transistors carries is therefore proportional to VB . With the high ohmic resistor R (indicated in Figure 25.8 with dotted lines), this maximum current corresponds

to either (VP – VSS – VTN)2 or (VDD – VQ – VTP)2, because in that situation no current flows through the resistor. Hence, with the extra resistor, it becomes possible to increase the maximum current in overdrive situations and therefore reduce the slewing time. Because resistor R is chosen to be high, it does not disturb the behavior of the circuit discussed previously. In practice, resistor R is replaced by transistor MR working in the triode region, as shown in Figure 25.9(a). Figure 25.9(b) shows the circuit which was used in Ref. [6] for biasing the gates of transistors M0, M9, and M11. It is much like the so-called replica biasing. The current in the circuit is strongly determined by the voltage across R (and its value) and is therefore very sensitive to variations in the supply voltage.

Adaptively Biased OTAs

Another combination of high available output current with low standby current can be realized by making the tail current of the differential input pair signal-dependent. Figure 25.10 shows the basic idea of such

an OTA with adaptive biasing [7]. The tail current I0 of the differential pair is the sum of a fixed value IR and an additional current equal to the absolute value of the difference between the drain currents multiplied by the current feedback factor B (I0 = IR + B|I1 – I2|). Therefore, with zero differential input voltage, only a low bias current IR flows through the input pair. A differential input voltage, Vind, will cause a difference in the drain currents which will increase the tail current. This, in turn, again gives rise to a greater difference in the drain current, and so on. This is the kind of positive feedback that can bring the differential input pair from the weak-inversion mode into the strong-inversion mode, depending on the input voltage and the chosen current feedback factor B.

Normally, when Vind = Vin+ – Vin– is small, the input transistors are in weak inversion. The differential output current (I1 – I2) of a differential pair operating in weak inversion equals the tail current times tanh((qVind)/(2AkT)). This leads to the following equation:

To keep some control over the output current, a negative overall feedback must be applied, which is usually the case. For example, when an OTA is used as a unity-gain buffer with a load of CL (see Figure 25.11) and assuming a positive input step is applied, then the output current increases dramatically due to the positive feedback action described previously and, as a result, the output voltage will increase. This will lead to a decrease of the differential input voltage Vind (Vind = Vs – Vout). The result will be a very fast settling of the output voltage, and that is what we wanted to have. To realize current |I1 – I2|, two current-subtracter circuits can be combined (see Figure 25.12). If the current I2 is larger than current I1, the output of current-subtracter circuit 1 (Iout1) will carry a current; otherwise, the output current will be zero. The opposite situation is found for the output current of subtracter circuit 2 because of the interchange of their input currents (Iout2 = B(I1 – I2)). Consequently, either Iout1 or Iout2 will draw a current B|I1 – I2| and the other current will be zero. It is for this reason that the upper current mirrors (in Figure 25.13) have two extra outputs to support the currents for the circuit in Figure 25.12. A practical realization of the adaptive-biasing OTA is shown in Figure 25.13. To avoid unwanted, relatively high standby currents due to transistors mismatches, the transfer ratio of the current mirrors (M12, M13) and (M19, M18) can be chosen somewhat larger than 1. This ensures an inactive region of the input voltage range whereby the feedback loop is deactivated.

Another example of an adaptive tail current circuit is shown in Figure 25.14 [8]. It has a normal OTA structure except that the input pair is realized in twofold, and the tail current transistor is used in a feedback loop. This feedback loop includes the inner differential pair and tail current transistor M0 as well as a minimum current selector, the current source IU, transistor MR, and a current sink IL. The minimum current selector [9] delivers an output current equal to the lowest value of its input currents (I¢out = Min(I¢1, I¢2)).

The feedback loop ensures that the output current of the minimum current selector is equal to the difference in currents between the upper and lower current sources. Assume that the upper current carries a current

2IB and the lower current source carries IB, then the feedback loop will bias the tail current in such a way that either I¢1 or I¢2 becomes equal to IB; for positive values of Vind, that will be I¢2. It should be realized that at Vind = 0, all four input transistors are biased at the same gate–source voltage (VGS0), corresponding to a drain current IB. In the case of positive input voltages, the gate–source voltage of M2/M¢2 will not change.

Therefore, all the input voltage will be added to the bias voltage of M1/M¢1, that is,

Figure 25.15 shows the ID versus VGS characteristic for both transistors M1/M¢1 and M2/M¢2. Accordingly, the relationship between (I1 – I2) versus Vind (for Vind > 0) follows the right side of the ID – VGS curve of M1, starting from the standby point (VGS0, IB) as indicated by the solid curve in Figure 25.15. A similar

view can be taken for negative values of the input voltage Vind, resulting in an equal (I1 – I2) versus Vin curve rotated 180°. The result is shown in Figure 25.16.

Note that this input stage has a relationship between (I1 – I2) and Vind that is different from that of a simple differential input stage. By increasing Vind, the slope increases and, to a first-order approximation, there will not be a limit for the maximum value of (I1 – I2).

Note that there is an additional MOS transistor MR in the circuit in Figure 25.14 to fix the output voltage of the minimum current selector circuit. The lower current source IL is necessary to be able to discharge the gate–source capacitor C of M0 (indicated in Figure 25.14 with dotted lines). The OTA in Figure 25.14 is simpler than that in Figure 25.13. However, its bandwidth is lower due to the high impedance of node P in the feedback loop.

Class AB OTAs

Another possibility to design an OTA with a good current efficiency is to use an input stage exhibiting class AB characteristics [10]. The input stage in Figure 25.17 contains two CMOS pairs [11] connected as Class AB input transistors. They are driven by four source followers. By applying a differential input voltage, the current through one of the input pairs will increase while the current through the other will decrease. The maximum current that can flow through the CMOS pair is, to first order, unlimited. In practice, it is limited by the supply voltage, the Keq factor, the mobility reduction factor, and the series resistance. The currents are delivered to the output with the help of two current mirrors. In the OTA shown in Figure 25.17, only one of the two outputs of each CMOS pair is used. The other output currents flow directly to the supply rails. Instead of wasting the other output currents, they can be used to supply an extra output. So with the addition of two current mirrors, an OTA with complementary outputs as shown in Figure 25.18 can be achieved [12]. An improvement of the output impedance and low-frequency voltage gain can be obtained by cascoding the output transistors of the current mirrors (Figure 25.19). Usually, this reduces the output window. The function of transistors M41–M44 is to control the DC output voltages. They form a part of a common-mode feedback system, which will be discussed next.

The relationship between the differential input voltage Vin and one of the output currents Iout is shown in Figure 25.20. There is a linear relationship between Vind and Iout for small to moderate values of Vind.

In the case of larger values of Vind, one of the CMOS pairs becomes cut off, resulting in a quasi-quadratic relationship. At a further increase of Vind, the output current will be somewhat saturated due to mobility reduction and to the fact that one of the transistors of the CMOS pair leaves saturation mode. The latter effect is, of course, also strongly dependent on the common input voltage.