Sequential Networks:Sequential Networks in Fundamental Mode.
Sequential Networks in Fundamental Mode
In a sequential network, the value of the network output depends on both the current input values and some of past input values stored in the network. We can find what value the output has for each individual combination of input values, depending on what signal values are stored in the network. This essentially means interpreting the signals stored inside the network as new input variables called internal variables and then interpreting the entire network as a combinational network of the new input variables, plus the original inputs, which are external input variables.
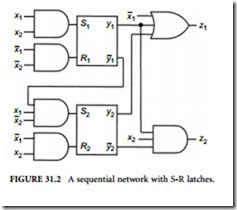
Let us consider the sequential network in Figure 31.2. Assume that the inputs are never changed unless the network is in a stable condition, that is, unless none of the internal variables is changing. Also assume that, whenever the inputs change, only one input changes at a time. Let y1, y1 , y2, and y2 denote the outputs of the two S-R latches.
Let us assume that y1 = y2 = 0 (accordingly, y1 = y2 = 1). x1 = 0, and x2 = 1. Then, as can be easily found, we have z1 = 1 and z2 = 0 for this combination of values. Because of x1 = 0 and x2 = 1, the inputs of the latches have values R2 = 1 (accordingly, y2 = 0) and S1 = S2 = R1 = 0. Then y1 and y2 remain 0. As long as x1, y1, and y2 remain 0 and x2 remains 1, none of the signal values in this network changes and, consequently, this combination of values of x1, x2, y1, and y2 is called a stable state.
Next let us assume that x1 is changed to 1, keeping x2 = 1 and y1 = y2 = 0. For this new combination of input values, we get z1 = 0 and z2 = 0 after a time delay of τ, where τ is the switching time (delay time) of each gate, assuming for the sake of simplicity that each gate has the same τ (this is not necessarily true in practice). The two latches have new inputs S1 = 1 and S2 = R1 = R2 = 0 after a time delay of τ.
Then, they have new output values y1 = 1 (previously 0), y1 = 0, y2 = 0, and y2 = 1 after a delay due to the response time of the latches. Outputs z1 and z2 both change from 0 to 1. After this change, the network does not change any further. Summarizing the above, we can say that, when the network has the combination x1 = x2 = 1, z1 = z2 = y1 = y2 = 0, the network does not remain in this combination, but changes into the new combination x1 = x2 = z1 = z2 = y1 = 1, y2 = 0. Also, outputs z1 and z2 change into z1 = z2 = 1, after assuming the values z1 = z2 = 0 temporarily. After the network changes into the
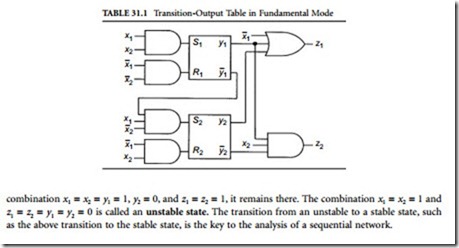
This and other transitions for other combinations of values of x1, x2, y1, y2, z1, and z2 can be shown on the map in Table 31.1, which is called a transition-output table, showing the next values of y1 and y2 as Y1 and Y2, respectively. The entry in each cell in Table 31.1 is next states Y1, Y2 and outputs z1 and z2. The above transition from x1 = 0, x2 = 1, y1 = y2 = 0 to x1 = x2 = y1 = 1, y2 = 0 is shown by the line with an arrow in Table 31.1. For this transition, the network is initially in the cell labeled with ∗ in Table 31.1; and when x1 changes to 1, the network moves to the next cell labeled with the dot with this cell’s entry, Y1 = 1, Y2 = 0, and z1 = z2 = 0, during the transient period. Here, it is important to notice that in this cell, next values of internal variables y1 and y2, i.e., Y1 and Y2 are shown but the network actually has current values of y1 and y2, that is, y1 = y2 = 0 during this transition period corresponding to this cell.
Y1 and Y2 in this cell, which is in an unstable state, indicates what values y1 and y2 should take after the transition. Then, the network moves to the bottom cell where the values of y1 and y2 are identical to Y1 and Y2, respectively, as indicated by the line with an arrow, because Y1 and Y2 will be current y1 and y2 after the transition. The present values of the internal variables are shown with y1 and y2 in small letters and their next values are with Y1 and Y2 in capital letters. More specifically, variables y1 and y2 are called present-state (internal) variables, and Y1 and Y2 are called next-state (internal) variables. As can easily be seen, when the values of Y1 and Y2 shown inside a cell are identical to those of y1 and y2 shown on the left of the table, respectively, a state containing these values of Y1, Y2, y1, and y2 is stable, because there is no transition of y1 and y2 into a new, different state. Next-state variables in stable states are encircled in Table 31.1. Each column in this table corresponds to a combination of values of network inputs x1 and x2, that is, an input state. Each row corresponds to a combination of values of internal variables y1 and y2, that is, a present internal state. Thus, each cell corresponds to a total state, or simply a state; that is, a combination of values of x1, x2, y1, and y2.
When only next states Y1 and Y2 are shown, instead of showing all next states Y1, Y2, and outputs z1 and z2 in each cell of a transition-output table, the table is called a transition table, and when only outputs z1 and z2 are shown, the table is called an output table.
Fundamental Mode
A sequential network is said to be operating in fundamental mode when the transition occurs horizontally in the transition table corresponding to each network input change and, then, unless the new state in the same row is stable, the transition continues vertically (not diagonally), settling in a new stable state, such as the transition shown with the line with an arrow in Table 31.1. The transitions of the network take place under the assumption that only one of the network inputs changes at a time, only when the network is not in transition; that is, only when the network is settled in a stable state.
By using a transition-output table, the output sequence [i.e., the sequence of output values corresponding to any input sequence, (i.e., the sequence of input values)] can be easily obtained. In other words, the output sequence can be obtained by choosing columns corresponding to the input sequence and then moving to stable states whenever states.


Comments
Post a Comment