Emitter-Coupled Logic:Standard ECL Logic Gates.

Introduction

ECL, which stands for emitter-coupled logic, is based on bipolar transistors and is currently the logic family with the highest speed and a high output power capability, although power consumption is also the highest. ECL is more complicated to fabricate, covers a larger chip area, and is more expensive than any other logic family. As the speed of CMOS improves, ECL is less often used but is still useful for the cases where high speed, along with large output power, are necessary, such as high-speed transmission over communication lines. ECL has three types of transistor circuits: standard ECL logic gates, their modification with wired logic, and ECL series-gating [4,6,10,13].

Standard ECL Logic Gates

A standard ECL logic gate is a stand-alone logic gate, and logic networks can be designed using many as building blocks. Its basic circuit is shown in Figure 38.1. ECL has unique logic capability, as explained in the following.

The logic operation of the ECL gate shown in Figure 38.1 is analyzed in Figure 38.2, where the input z in Figure 38.1 is eliminated for simplicity. The resistors connected to the bases of transistors, Tx and Ty , are for protecting these transistors from possible damage due to heavy currents through a transistor, but not for logic operations, and can be eliminated if there is no possibility for an excessively heavy current to flow. When input x has a high voltage representing logic value 1 and y has a low voltage representing logic value 0, transistor Tx becomes conductive, Ty becomes non-conductive, and a current flows through Tx and resistor R1, as illustrated in Figure 38.2(a). In this case the voltage at the emitter of transistor Tr becomes higher than –4 V due to the current through resistor Rp, as shown. Consequently, the voltage at this emitter becomes higher and the voltage at its base becomes not sufficiently high against its emitter to make Tr conductive, so there is no current through Tr and resistor R2. Consequently, transistor Tf has a high voltage at its base, which makes Tf conductive, and output f has a high voltage representing logic value 1. On the other hand, transistor Tg is almost non-conductive (actually a small

current flows, but let us ignore it for simplicity), since its base has a low voltage due to the voltage drop developed across resistor R1 by the current shown. Thus, output g has a low voltage representing logic value 0.

Even when y (instead of x), or both x and y, has a high voltage, the above situation is not changed, except for the current through Ty .

Next, suppose that both inputs x and y have low voltages, as shown in Figure 38.2(b). Then there is no current through resistor R1. Since the base of transistor Tr has a higher voltage than its emitter (0 V at the base and –0.8 V at the emitter), a current flows through R2 and Tr , as illustrated in Figure 38.2(b). Thus, Tf has a low voltage at its base and becomes almost non-conductive (more precisely speaking, less conductive). Output f has, consequently, a low voltage, representing logic value 0. Transistor Tg has a high voltage at its base and becomes conductive. Thus, output g has a high voltage, representing logic value 1.

Therefore, a current flows through only one of R1 and R2, switching quickly between these two paths. Notice that resistor Rp in Figure 38.2 which is connected to a power supply of minus voltage is essential for this current steering because the voltage at the top end of Rp determines whether Tr becomes conductive or not. The emitter followers (shown in the dot-lined rectangles in Figure 38.1) can deliver heavy output currents because an output current flows only through either transistor Tf or Tg and the on-resistance of the transistor is low.

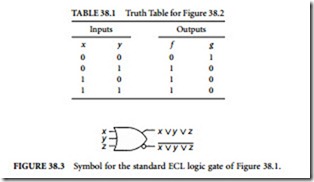
The above analysis of Figure 38.2 leads to the truth table in Table 38.1. From this table, the network in Figure 38.2 has two outputs: f = x ∨ y and g= x ∨ y .

In a similar manner, we can find that the ECL gate in Figure 38.1 has two outputs: f = x ∨ y ∨ z and g= x ∨ y ∨ z .

The gate is denoted by the symbol shown in Figure 38.3. The simultaneous availability of OR and NOR as the double-rail output logic, with few extra components, is the unique feature of the ECL gate, making its logic capability powerful.

Emitter-Dotting

Suppose we have the emitter follower circuit shown in Figure 38.4(a) (also shown in the dot-lined rectangles in Figure 38.1), as part of an ECL logic gate. Its output function, f, at the emitter of the bipolar transistor is 1 when the voltage at the emitter is high (i.e., the bipolar transistor in (a) is conductive), and f is 0 when the voltage at the output terminal is low (i.e., the bipolar transistor in (a) is non-conductive). Then, suppose there is another alike circuit whose output function at the emitter is g. If the emitters of these two circuits are tied together as shown in Figure 38.4(b), the new output function at the tied point is h = f ∨ g, replacing the original functions, f and g. This connection is called emitter-dotting, realizing Wired-OR. The tied point represents the new function f ∨ g because if both transistors, T1 and T2, are non-conductive, the voltage at the tied point is low; otherwise (i.e., if one of T1 and T2, or both, is conductive), the voltage at the tied point is high.

Wired-OR is an important feature of the ECL gate. The ECL gate in Figure 38.1 has two emitter followers: one for f and the other for g. As shown in Figure 38.5, the OR of the outputs can be realized without using an extra gate, simply by tying together these outputs. This is very convenient in logic design. If one output is Wired-ORed with another ECL gate, it does not express the original function. And it cannot be further Wired-ORed to other gates if we want to realize Wired-OR with the original function. But if the same output is repeated by adding an emitter follower inside the gate, as shown in Figure 38.6 (i.e., the emitter follower inside a dot-lined rectangle in Figure 38.1), then the new output can be Wired-ORed with another gate output or connected without Wired-OR to the succeeding gates.

In the ECL gate at the top position in Figure 38.6, for example, the first output f = x ∨ y ∨ z is connected to gates in the next level, while the same f in the second output is used to produce the output u ∨ v ∨ x ∨ y ∨ z by Wired-ORing with the output of the second ECL gate.

Design of a Logic Network with Standard ECL Gates

An ECL gate network can be designed, starting with a network of only NOR gates, for the following reason. Consider a logic network of ECL logic gates shown in Figure 38.7(a), where Wired-ORs are included. This network can be converted into the network without Wired-OR shown in (b) by directly connecting connections in each Wired-OR to the inputs of a NOR gate without changing the outputs at gates 4 and 5, possibly sacrificing the maximum fan-in restriction. Then, two NOR outputs of

gate 2 in (a), for example, can be combined into one in (b). Then, this network can be converted into the network shown in (c) by eliminating OR outputs of all gates 1, 2, and 3 in (b), and connecting inputs of these gates directly to gates 4 and 5. Thus, the network in (c) that expresses the same outputs as the network in (a) consists of NOR gates only (i.e., the outputs of gates 4 and 5 in (c) are the same as those in (a)), possibly further sacrificing the maximum fan-in restriction at some gates. Notice that in this conversion, the number of gates does not change or decreases (if an ECL gate, like gate 1 in (c), has no outputs used, it can be deleted from (c)). Thus, from the given network of standard ECL gates with Wired-ORs, we can derive a NOR network of the same or fewer number of gates, possibly with greater fan-in at some gates, as shown in Figure 38.7(d). Even if each gate has many NOR outputs or OR outputs, the situation does not change.

When we want to design a minimal standard ECL gate network for given functions f and f , it can be designed by reversing the preceding conversion, as follows.

Procedure 38.1: Design of logic networks with standard ECL logic gates

1. Design a network for a given logic function f and another network for its complement, f using NOR gates only without considering maximum fan-in or fan-out restriction at each gate. Use a minimum number of NOR gates in each case. (The map-factoring method described in Chapter 31 is usually convenient for manual design of logic networks with a minimum number of NOR gates in single- or double-rail input logic.)

2. Choose one among the two logic networks obtained. Reduce the number of input connections to each gate, by providing Wired-ORs, or by using OR-outputs of other gates, if possible. In this case, extra NOR or OR outputs at each ECL gate must be provided whenever necessary (like the reverse conversion from Figure 38.7(b) to Figure 38.7(a), or from Figure 38.7(c) to Figure 38.7(b)). Thus, if any gate violates the maximum fan-in restriction, we can try to avoid it by using Wired- ORs or OR outputs.

3. This generally reduces fan-out of gates also; but if any gate still violates the maximum fan-out restriction, try to avoid it by using extra ECL gates (no simple good methods are known for doing this). The output ECL gate of this network presents f and f .

If no gate violates the maximum fan-in and fan-out restrictions in Steps 2 and 3, the number of NOR gates in the original NOR network chosen in Step 2 is equal to the number of ECL gates in the resultant ECL network. So, if we originally have a network with a minimum number of NOR gates, the designed ECL network also has the minimum number of standard ECL logic gates. But extra ECL gates have to be added if some gates violate the maximum fan-in restriction, maximum fan-out restriction, or other constraints.

4. Repeat Steps 2 and 3 for the other network. Choose the better one. D Notice that the use of OR outputs and Wired-ORs generally reduces the number of connections or fan- ins (i.e., input transistors) and also reduces the total sum of connection lengths, thus saving chip area. For example, the total length of the connections for x and y in Figure 38.7(c) can be almost twice the connection length between two gates in Figure 38.7(b). Also, the total length of two connections in Figure 38.7(b) can be almost twice the length for Wired-OR in Figure 38.7(a). In Procedure 38.1, NOR networks with a minimum number of gates are important initial networks. It is known that when the number of gates is minimized, the number of connections in the networks also tends to be minimized [11]. (For the properties of wired logic, see Ref. 7.)