Dividers:Higher Radix Subtract-and-Shift Dividers.

Higher Radix Subtract-and-Shift Dividers

In the previous subsection, we considered radix-2 dividers. In this subsection, let us consider higher radix dividers. When the radix r is 2k, the number of iterations of the recurrence step is n/k. The larger the k, the fewer the iterations but the longer the time of each recurrence step, because of the additional complexity in the quotient-digit selection and the generation of the divisor multiples.

A redundant digit set, especially a redundant symmetric signed-digit set {–a, –a + 1, … , –1, 0, 1, … , a – 1, a}, where a ³ r/2, is often used to obtain fast algorithms. A larger a reduces complexity of the quotient-digit selection but increases the complexity of the generation of the divisor multiples. The use of the signed-digit set makes the conversion of the quotient into the ordinary binary representation necessary. The partial remainder can be represented in either non-redundant form, or redundant form (e.g., carry save form). By the use of a redundant form, we can perform addition/subtraction without carry/borrow propagation, and hence fast. However, it slightly complicates the quotient-digit selection and doubles the number of register bits required for storing the partial remainder.

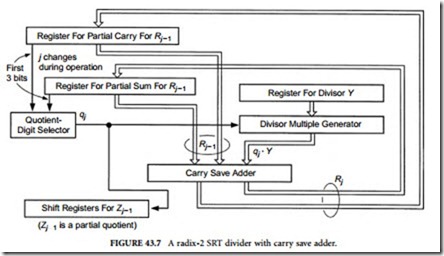
Among the radix-4 methods, the method with the quotient-digit set of {–2, –1, 0, 1, 2} and the redundant partial remainder is the most popular, because the generation of the divisor multiples is easy and carry save addition can be used for speed-up. In this method, Rj , which satisfies –(2/3)Y £ Rj < (2/3)Y, is represented in the carry save form (or redundant binary representation with the digit set {–1, 0, 1}) with 1-bit integral part (and n-bit fractional part). (R0 = X and X < (2/3)Y must hold.) Quotient digit qj is determined from the seven most significant digits of Rj –1 and the five most significant bits of Y. (Actually not five but four bits of Y are required, since its most significant bit is always 1.) The on-the-fly conversion of the quotient can be extended to radix-4. The essential part of a divider based on this method is very similar to that shown in Figure 43.7. The seven most significant bits of the content of Register For Partial Carry For Rj –1 and Register For Partial Sum For Rj –1, as well as the five (actually four) significant bits of the content of Register For Divisor Y are fed to Quotient Digit Selector. Divisor Multiple Generator generates –2Y, –Y, 0, Y, and 2Y. This type of divider is used in floating point arithmetic units of several microprocessors.

An efficient radix-8 method is with the quotient-digit set of {–7, –6, … , –1, 0, 1, … , 6, 7} and the redundant partial remainder. Quotient digit qj is determined from the eight most significant digits of Rj –1 and the four most significant bits of Y. Quotient digit qj is decomposed into two components, qhj Î {–8, –4, 0, 4, 8} and qlj Î {–2, –1, 0, 1, 2}, and Rj is calculated through two carry save additions.

As the radix increases, the quotient-digit selection becomes more complex. This complexity can be reduced by restricting the divisor to a range close to 1, by prescaling the divisor. We can preserve the value of the quotient by prescaling the dividend with the same factor as the divisor. For example, we can design an efficient radix-16 method with the quotient-digit set of {–10, –9, … , –1, 0, 1, … , 9, 10}, where qj is determined from the ten most significant digits of Rj –1, by scaling the divisor into (8107/8192) £ Y £ (8288 /8192). In this method, qj is decomposed into two components, qhj Î {–8, –4, 0, 4, 8} and qlj Î{–2, –1, 0, 1, 2}, and Rj is calculated through two carry save additions.

Since the recurrence step becomes more complex as the radix increases, a higher radix division step

by not merely concatenating lower radix stages but overlapping them so that the delay and the cost of the hardware for the recurrence step are reduced.