Adders:Ripple Carry Adder

Ripple Carry Adder

A parallel adder performs addition at all bit positions simultaneously, so it is faster than serial adders.

The simplest parallel adder is a ripple carry adder. An n-bit ripple carry adder is constructed by cascading n full adders, as shown in Figure 41.4. The carry output of each FA is connected to the carry input of the FA of the next higher position. The amount of its hardware is proportional to n. Its worst- case delay is proportional to n because of ripple carry propagation. In designing an FA for a fast ripple carry adder, it is critical to minimize the delay from the carry-in, ci, to the carry-out, ci+1.

An FA can be realized with logic gates, such as AND gates, OR gates, and XOR gates, as exemplified in Figure 41.3, and also can be realized with MOSFETs, including pass transistors [18,23], such that a carry ci goes through logic gates which have some delays. But the speed of adders is very important for

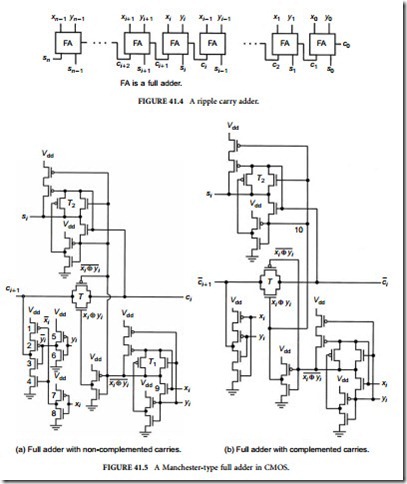
the speed of the entire computer. So, FAs are usually realized with more sophisticated transistor circuits using MOSFETs such that a carry ci can propagate fast to higher bit positions through pass transistors [22]. An example of such an adder is shown in Figure 41.5, being realized in CMOS. In Figure 41.5(a), a carry propagates through transmission gate, T (described in Chapter 39, Section 39.2). When we have xi = yi = 0, T becomes non-conductive and nMOSFETs, 3 and 4, become conductive. Then, the carry- out, ci+1, becomes 0 because the carry-out terminal ci+1 is connected to the ground through 3 and 4. When xi = yi = 1, T becomes non-conductive and pMOSFETs, 1 and 2, become conductive. Then, the carry-out, ci+1, becomes 1 because the carry-out terminal ci+1 is connected to the power supply Vdd through 1 and 2. When xi = 0 and yi = 1, or xi = 1 and yi = 0, T becomes conductive and the carry-out terminal is connected to neither Vdd nor the ground, so a carry-in ci is sent to ci+1 as a carry-out. Thus, we have the values of ci+1 for different combinations of values of xi, yi, and ci, as shown in Table 41.1. This carry-path is called a Manchester carry chain. (T1 is another transmission gate, whereby a circuit on the carry path is simplified and carry propagation is sped up and nMOSFET 9 works as a pass transistor.) A ripple carry adder with Manchester carry chain is referred to as Manchester adder. This idea combines very well with the carry skip technique to be mentioned in Section 41.5.

The FA in Figure 41.5(a) cannot send a carry over many positions in a ripple carry adder. For speed- up, we need to insert an inverter in every few positions to send a high output power over many higher bit positions. In order to reduce the number of inverters which have delays in themselves, we can use the FA shown in Figure 41.5(b) which works with complemented carries. An example with insertion of an inverter at the end of every four cascaded FAs is shown in Figure 41.6, where a block of four of Figure 41.5(a) and a block of four of Figure 41.5(b) are alternated. In Figure 41.5(b), inverters consisting of MOSFETS 5, 6, 7, and 8 are eliminated from (a), and the function xi ⊕ yi at point 10 in (b) is the complement of the function at the corresponding point in (a).

For high speed, a Manchester full adder realized in dynamic CMOS is used instead of the Manchester full adder shown in static CMOS, where dynamic CMOS and static CMOS are two different variations of CMOS. For example, a Manchester full adder in dynamic CMOS is used inside an adder (to be mentioned later) which is more complex but faster than ripple carry adders [7].

In the simultaneous addition in all n-bit positions, a carry propagates n positions in the worst case, but on the average, it propagates only about log2 n positions [13]. The average computation time of a ripple carry adder can be reduced by detecting the carry completion, because we need not always wait for the worst delay. An adder with such a mechanism is called a carry completion detection adder [3] and is useful for asynchronous systems.

When an FA is realized with ordinary logic gates, say NOR gates only, the total number of logic gates in the ripple carry adder is not minimized, even if the number of logic gates in each FA is minimized. But the number of logic gates in the ripple carry adder can be reduced by using modules that have more than one input for a carry-in (the carry-in ci, for example in Figure 41.7 is represented by two lines, instead of one line) and more than one output for a carry-out (the complemented carry-out ci +1 in Figure 41.7 is represented by three lines), as shown in Figure 41.7 (where modules are shown in dot-lined rectangles), instead of using FAs which have only one input for a carry-in and only one output for a carry-out. The number of NOR gates of such a module is minimized by the integer-programming logic design method [11] and it is found that there are 13 minimal modules. Different types of ripple carry adders can be realized by cascading such minimal modules. Some of these adders have carry propagation times shorter than that of the ripple carry adder realized with FAs with NOR gates. Besides, there is an adder that has a minimum number of NOR gates—when this adder is constructed by cascading the three consecutive minimal modules shown in dot-lined rectangles in Figure 41.7, where the module for the least significant bit position is slightly modified (i.e., replacement of the two carry inputs by a single carry input) and one NOR gate is added to convert the carry out in multiple-lines from the adder into the carry out in a single line. Then it is proved that the total number of NOR gates in this ripple carry adder is minimum for any value of n [8]. Also, there is a ripple adder such that the number of connections, instead of the number of logic gates, is minimized [14]. Related adders are referred to in Section 2.4.3 of Ref. 11.

FIGURE 41.7 Three consecutive minimal modules for a ripple carry adder that has the minimal number of NOR gates for any arbitrary bit length.