Adders:Carry Look-Ahead Adder.
Carry Look-Ahead Adder
As previously stated, the carry, ci+1, produced at the i-th position is calculated as ci+1 = xi ·yi ∨ ci ·(xi ⊕ yi). This means that a carry is generated if both xi and yi are 1, or an incoming carry is propagated if one of xi and yi is 1 and the other is 0. Therefore, letting gi denote xi yi, we have ci+1 = gi ∨ ci pi, where pi = xi ⊕ yi.
Here, gi is the formula for the carry generation condition at the i-th position, i.e., when gi is 1, a carry is generated at this position. Substituting gi–1 ∨ pi–1ci–1 for ci, we get
A carry look-ahead adder can be realized according to this expression, as illustrated in Figure 41.10 for the case of four bits [21]. According to this expression, ci+1’s are calculated at all positions in parallel. It is hard to realize an n-bit carry look-ahead adder precisely according to this expression, unless n is small, because maximum fan-in and fan-out restriction is violated at higher positions. Large fan-out causes large delay, so the maximum fan-out is restricted. Also, the maximum fan-in is usually limited to 5 or less. There are some ways to alleviate this difficulty, as follows.
One way is the partition of carry look-ahead adders into several blocks such that each block consists of k positions, starting from the j-th one. In a block h, the carry at each position, ci+1, where j ≤ i ≤ j + k – 1, is calculated as
where Ch, i.e., cj is the carry from the next lower block. The carry from the next lower block, Ch, goes to only the positions of the block h, so the fan-outs and fan-ins do not increase beyond a certain value. Therefore, we can form an n-bit adder by cascading n/k k-bit carry look-ahead adders, where k is a small constant independent of n, often 4. The worst delay of this type of adder and also the hardware amount are proportional to n.
Another way of alleviating the difficulty is recursively applying the principle of carry look-ahead to groups of blocks. The carry output of block h, Ch+1 (= cj+k ), is calculated as
is 1, and an incoming carry is propagated if Ph = pj+k–1 pj +k–2 … pj +1 pj is 1. Gh is the formula for the carry generation condition of the block and Ph is the formula for the carry propagation condition of the block. (They are shown as P and G in Figure 41.10) Let us consider a super-block, that is, a group of several consecutive blocks. The carry generation and the carry propagation condition of a super-block are detected from those of the blocks, in the same way that Gh and Ph are detected from gi’s and pi’s. Once the carry input to a super-block is given, carry outputs from the blocks in the super-block are calculated immediately. Consequently, we obtain a fast adder in which small carry look-ahead circuits which include carry calculation circuits are connected in a tree form. Figure 41.11 shows a 4-bit carry look-ahead circuit and Figure 41.12 shows a 16-bit carry look-ahead adder using the 4-bit carry look-ahead circuits, where carry look-ahead circuits are shown as CLA in Figure 41.12. The worst delay of this type of adder is proportional to log n. The number of logic gates is proportional to n.

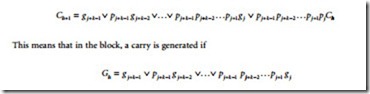




Comments
Post a Comment