Sequential Networks:Synthesis of Sequential Networks.

Synthesis of Sequential Networks

Since the use of clocks has many advantages, synchronous sequential networks with clocks are in many cases preferred to asynchronous sequential networks. In addition to the ease of design and elimination of hazards including racing problems, the speed of logic networks can sometimes (e.g., Domino CMOS) be improved by synchronizing the operations of logic gates by clocks, and waveforms of signals can be reshaped into clean ones.

For synchronous sequential networks, more sophisticated flip-flops than latches are usually used, along with clocks. With these flip-flops, which are called raceless flip-flops, network malfunctioning due to hazards can be completely eliminated. Design of sequential networks with raceless flip-flops and clocks is much simpler than that of networks in fundamental mode, since we can use simpler flow-output and state-output tables, which are said to be in skew mode, and multiple changes of internal variables need not be avoided in assigning binary numbers to states.

Raceless Flip-Flops

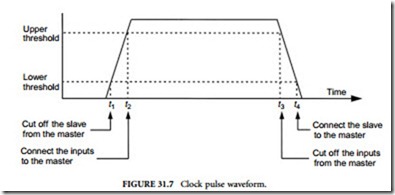
Raceless flip-flops are flip-flops that have complex structures but eliminate network malfunctions due to races. Most widely used raceless flip-flops are master-slave flip-flops and edge-triggered flip-flops. A master-slave flip-flop (or simply, an MS flip-flop) consists of a pair of flip-flops called a master flip- flop and a slave flip-flop. Let us explain the features of master-slave flip-flops based on the J-K master- slave flip-flop shown in Figure 31.5. For the sake of simplicity, all the gates in these flip-flops are assumed to have equal delay times, although in actual electronic implementations, this may not be true. Its symbol is shown in Figure 31.6, where the letters MS are shown inside the rectangle. Each action of the master- slave flip-flop is controlled by the leading and trailing edges of a clock pulse, as explained in the following. The J-K master-slave flip-flop in Figure 31.5 works with the clock pulse, as illustrated in Figure 31.7, where the rise and fall of the pulse are exaggerated for illustration. When the clock has the value 0 (i.e., c = 0) NAND gates 1 and 2 in Figure 31.5 have output values 1, and then the flip-flop consisting of gates 3 and 4 does not change its state. As long as the clock stays at 0, gates 5 and 6 force the flip-flop consisting of gates 7 and 8 to assume the same output values as those of the flip-flop consisting of gates 3 and 4 (i.e., the former is slaved to the latter, which is the master). Each of the master and slave is a slight modification of the latch in Figure 31.1(d).

When the clock pulse starts to rise to the lower threshold at time t1 in Figure 31.7, gates 5 and 6 are disabled: in other words, the slave is cut off from the master. (The lower threshold value of the clock pulse still presents the logic value 0 to gates 1 and 2. The clock waveform is inverted to gates 5 and 6 through the inverter. The inputs to gates 5 and 6 from the inverter present the logic value 0 also to gates 5 and 6, because the inverted waveform is still close to logic value 1 but is not large enough to let gates 5 and 6 work. The inverter is actually implemented by a diode which is forward-biased, so that the network works in this manner.) When the clock pulse reaches the upper threshold at t2, (i.e., c = 1), gates 1 and 2 are enabled, and the information at J or K is read into the master flip-flop through gate 1 or 2. Since the slave is cut off from the master by disabled gates 5 and 6, the slave does not change its state, maintaining the previous output values of Q and Q . When the clock pulse falls to the upper threshold at t3 after its peak, gates 1 and 2 are disabled, cutting off J and K from the master. In other words, the outputs of 1 and 2 become 1, and the master maintains the current output values. When the clock pulse falls further to the lower threshold at t4, gates 5 and 6 are enabled and the information stored at the master is transferred to the slave, gates 7 and 8.

The important feature of the master-slave flip-flop is that the reading of information into the flip-flop and the establishment of new output values are done at different times; in other words, the outputs of the flip-flop can be completely prevented from feeding back to the inputs, possibly going through some gates outside the master-slave flip-flop, while the network that contains the flip-flop is still in transition. The master-slave flip-flop does not respond to its input until the leading edge of the next clock pulse. Thus, we can avoid oscillatory races. Now we have a J-K flip-flop that works reliably, regardless of how long a clock pulse or signal 1 at terminal J or K lasts, since input gates 1 and 2 in Figure 31.5 are gated by output gates 7 and 8, which do not assume new values before gates 1 and 2 are disconnected from J and K. As we will see later, sequential networks that work reliably can be constructed compactly with master-slave flip-flops, without worrying about hazards.

Other types of master-slave flip-flops are also used. The T (type) master-slave flip-flop (this is also called toggle flip-flop, trigger flip-flop, or T flip-flop) has only a single input, labeled T, as shown in Figure 31.8(a), which is the J-K master-slave flip-flop with J and K tied together as T. Whenever we have T = 1 during the clock pulse, the outputs of the flip-flop change, as shown in Figure 31.8(b). The T-type flip-flop, denoted as Figure 31.8(c), is often used in counters. The D (type) master-slave flip-flop (D implies “delay”) has only a single input D, and is realized, as shown in Figure 31.9(a). As shown in Figure 31.9(b), no matter what value Q has, Q is set to the value of D that is present during the clock pulse. The D-type flip-flop is used for delay of a signal or data storage and is denoted by the symbol shown in Figure 31.9(c).

Edge triggered flip-flops are another type of raceless flip-flop. Either the leading or the trailing edge of a clock pulse (not both) causes a flip-flop to respond to an input, and then the input is immediately disengaged from the flip-flop. Edge-triggered flip-flops are mostly used in the same manner as master- slave flip-flops.

Example of Design of a Synchronous Sequential Network

Let us now explain synthesis of a synchronous sequential network with an example.

Specification for the Design Example

Suppose we want to synthesize a clocked network with two inputs, x1 and x2, and single output z under the following specifications:

1. Inputs do not change during the presence of clock pulses, as illustrated in Figure 31.10. Inputs x1 and x2 cannot assume value 1 simultaneously during the presence of clock pulses. During clock pulses, an input signal of value 1 appears at exactly one of two inputs, x1 and x2, of the network, or does not appear at all.

2. The value of z changes as follows.

a. The value of z becomes 1 when the value 1 appears during the clock pulse at the same input at which the last value 1 appeared. Once z becomes 1, z remains 1 regardless of the presence or absence of clock pulses, until signal 1 starts to appear at the other input during clock pulses. (This includes the following case. Suppose that we have z = 0, when signal 1 appears at one of the inputs during a clock pulse. Then, signal 0 follows at both x1 and x2 during the succeeding clock pulses. If signal 1 comes back to the same input, z becomes 1.) As illustrated in Figure 31.10, z becomes 1 at time t1 at the leading edge of the second pulse because signal 1 is repeated at input x1. Then z continues to remain 1 even though signal 1 appears at neither input at the third pulse starting t2.

b. The value of z becomes 0 when the value 1 appears at the other input during the clock pulse.

Once z becomes 0, z remains 0 regardless of the presence or absence of clock pulses, until signal 1 starts to appear at the same input during clock pulses. In Figure 31.10, z continues to be 1 until the leading edge of the pulse starting at time t3. Then z continues to remain 0 until the time t4.

Let us prepare a flow-output table for this design problem in the following steps.

1. An output value of z must depend on an internal state only, because z has to maintain its value until next change. Let us assume that there are exactly two states, A and B, such that z = 0 when the network is in state A and z = 1 when the network is in state B. (We will try more than two states if two are found insufficient.)

2. Assume that during the absence of a clock pulse, the network is in state A. Let c denote the clock.

Since the network must stay in this state as long as c = 0, the next state, S, in the column for c = 0 must be A, as shown in Table 31.10(a). Similarly, the next state for the second row in the column c = 0 must be B. It is to be noted that during c = 0, there are four combinations of values of x1 and x2 (i.e., x1 = x2 = 0; x1 = 1 and x2 = 0; x1 = 0 and x2 = 1; and x1 = x2 = 1). But the states of the network to be synthesized is irrelevant of the values of x1 and x2. Thus, in Table 31.10, we have only one column corresponding to c = 0, instead of four columns.

3. When the network is in state A during c = 0, suppose that we have x1 = 1 at the next clock pulse.

Let us choose A as the next state, S, as shown in the last column in Table 31.10(a). But this choice means that, if we apply value 1 repeatedly at x1, the network goes back and forth between the two states in the first and last columns in the first row in Table 31.10(a). Then z = 1 must result from the specification of the network performance; but since the network stays in the first row, we must have z = 0. This is a contradiction. Thus, the next state for (x1, x2, s) = (10A) cannot be A.

4. Next assume that the next state for (x1, x2, s) = (10A) is B, as shown in Table 31.10(b). Suppose that the value 1 has been alternating between x1 and x2. If we had the last 1 at x2, the network must be currently in A because of z = 0 for alternating 1’s. When the next 1 appears at x1, z = 0

must still hold because the value 1 is still alternating. But the network will produce z = 1 for state (10A), because B is assumed to correspond to z = 1. This is a contradiction, and the choice of B is also wrong.

5. In conclusion, two states are not sufficient, so we try again with more states. For this example, considering only two states corresponding to z = 0 and 1 is not appropriate.

6. In the above, we had contradictions by assuming only two states, A and B, corresponding to z = 0 and 1; we did not know which input’s 1 led to each state. Thus, in addition to the values of z, let us consider which input had the last 1. In other words, we have four states corresponding to the combinations of z and the last 1, as shown in Table 31.11. At this stage, we do not know whether or not three states are sufficient. But let us assume four states for the moment. As a matter of fact, both three states and four states require two internal variables. Hence, in terms of the number of internal variables, it does not matter whether we have three or four states, although the two cases may lead to different networks.

7. Derivation of a flow-output table in skew mode: Let us form a flow-output table, assuming the use of J-K master-slave flip-flops. In the column of c = 0 in Table 31.11, the network must stay in each state during the absence of a clock pulse. Thus, all the next states S in all the cells in the column of c = 0 must be identical to s in each row. Suppose that the network is in state (c, x1, x2, s) = (000A) with output z = 0 after having the last 1 at x1. When the value 1 appears at x1 and c becomes 1, the next state S must be B for the following reason. When the current clock pulse disappears, this 1 at x1 will be “the last 1” at x1 (so S must be A or B) and z will have to be 1 because of the repeated occurrence of 1’s at x1. (This contradicts z = 0, which we will have if A is entered as S.) Hence, the possibility of S being A is ruled out, and S must be B. Since value 1 is repeated at x1, we have z = 1. The next states and the values of output z in all other cells in Table 31.11 can be found in a similar manner.

Let us analyze how a transition among stable states occurs in this table. According to the problem specification, inputs x1 and x2 can change only during the absence of clock pulses.

Suppose that during the absence of a clock pulse, the network is in state (c, x1, x2, s) = (000A) in Table 31.11. Suppose that inputs (x1, x2) change from (00) to (10) sometime during the absence of a clock pulse and (x1, x2) = (10) lasts at least until the trailing edge of the clock pulse. If this transition is interpreted on Table 31.11, the network moves from (c, x1, x2, s) = (000A) to (110A), as shown by the dotted-line with an arrow, at the leading edge of the clock pulse. Then the network must stay in this state, (110A), until the trailing edge of the clock pulse, because the outputs of the J-K master-slave flip-flops keep the current values during the clock pulse, changing to its new values only at the trailing edge of the clock pulse and thus the internal state s does not change yet to its new state S. (This is different from the fundamental mode, in which the network does not stay in this state unless the state is a stable one, and vertically moves to a stable state in a different row in the same column.) Then the network moves from (c, x1, x2, s) = (110A) to (010B), as shown by the solid-line with an arrow in Table 31.11, when s assumes the new state S at the trailing edge of the clock pulse. Thus, the transition occurs horizontally and then diagonally in

Notice, however, that in the new state (110A) at the leading edge of the clock pulse in the above transition from (c, x1, x2, s) = (000A), the network z assumes the new output value. Consequently, in this new stable state during c = 1 in Table 31.11, the new current value of the network output, z, is shown, while the value of the internal state in this new stable state shows the next state S, though the network is actually in s. In the fundamental mode, when the network moves horizon- tally to a new unstable state in the same row in the state-output table, the current value of the network output is shown and the internal state represents the next state, S (in this sense the situation is not different), but the network output lasts only during a short, transient period, unless the new state is stable. In contrast, in skew mode, the output value for the new state is not transient (because the network stays in this state during the clock pulse) and is essential in the description of the network performance.

Let us synthesize a network for this flow-output table in skew mode later.

8. Derivation of a flow-output table in fundamental mode: Next let us try to interpret this table in fundamental mode. Table 31.11 shows that, when the network placed in state (c, x1, x2, s) = (000A) receives x2 = 1 before the appearance of the next pulse, the next state will be C at the leading edge of the next pulse. But the network goes to unstable state (c, x1, x2, s) = (101C) that has entry D, since if we assume fundamental mode, it must move vertically, instead of the diagonal transition in skew mode. Hence, the network must go further to stable state (101D), without settling in the desired stable state, C, if the network still keeps x2 = 1 and c = 1. Therefore, the network cannot be in fundamental mode. (Recall that the next state entries in a flow-output table, unlike a state- output table, do not show intermediate unstable states but do show the destination stable states.) The above difficulty can be avoided by adding two new rows, E and F, as shown in Table 31.12. When the network placed in state (c, x1, x2, s) = (000A) receives x2 = 1, the network goes to the new stable state F in column (x1, x2) = (01) and in row F. For this state F, z = 0, without causing contradiction. When the clock pulse disappears, the network goes to stable state (000C) after passing through unstable state (000F). The problem with the other states is similarly eliminated. All stable states are encircled as stable states.

The values of z for stable states are easily entered. The values of z for unstable states can be entered with certain freedom. For example, suppose that the network placed in state (c, x1, x2, s) = (000A) receives x1 = 1. Then the next state S is B. In this case, we may enter 0 or 1 as z for (110A) for the following reason. We have z = 0 for the initial stable state A during c = 0 and z = 1 for the destination stable state B during c = 1 and correspondingly z = 0 or 1. This does not make much difference as far as the external behavior of the network is concerned, because the network stays

in this unstable state (110A) for the short transient period and it simply means that z = 1 appears a little bit earlier or later. The network that results, however, may be different. Accordingly, z = d (d denotes “don’t-care”) would be the best assignment, since this gives flexibility in designing the network later.

Design of Synchronous Sequential Networks in Skew Mode Now let us design a synchronous sequential network based on a flow-output table in skew mode, using master-slave flip-flops.

As pointed out previously, when master-slave flip-flops are used, the network does not have racing hazards even if internal variables make multiple changes, because the flip-flops do not respond to any input changes during clock pulses. Thus, we need not worry about hazards due to multiple changes of internal variables and consequently appropriate assignment of binary numbers to states in forming a transition-output table from a state-output table or a flow-output table in the design steps in Figure 31.4. But the number of gates, connections, or levels in a network to be designed can differ, depending on how binary numbers are assigned to states (it is of secondary importance compared with the hazard problem, which makes networks useless if they malfunction). Making state assignments without considering multiple changes of internal variables is much easier than having to take these changes into account. Let us derive the transition-output table shown in Table 31.13 from Table 31.11, using a state assignment as shown.

Reversing the inputs and outputs relationship of J-K master-slave flip-flops shown in Table 31.14(a), we have the output-input relationship shown in Table 31.14(b) (other master-slave flip-flop types can be treated in a similar manner). Table 31.14(b) shows what values inputs J and K must take for each change of internal variable y to its next value Y. (In order to have y = Y = 0, J = K = 0 or J = 0 and K = 1 must hold, as we can see in Table 31.14(a) and thus we have S = 0 and R = d in Table 31.14(b).) Using

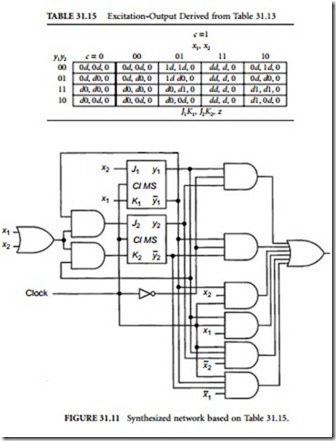
Table 31.14(b), we form the excitation table in Table 31.15. Decomposing Table 31.15 into five Karnaugh maps for J1, K1, J2, K2 and z, we can find a minimal sum for each of J1, K1, J2, K2, and z. On the basis of these logic expressions, we design the loopless network inside the general model of sequential networks in Figure 31.3. Then, placing two J-K master-slave flip-flops outside this loopless network, we have designed the sequential network shown in Figure 31.11.

Master-slave flip-flops do not respond to changes in their inputs when and after their outputs change until the leading edges of next clock pulses. Thus, no network malfunction due to races occurs, and no post-analysis of whether or not the designed networks malfunction due to this is necessary. This is the advantage of clocked networks with raceless flip-flops.

Design of Asynchronous Sequential Networks in Fundamental Mode Now let us design an asynchronous sequential network based on a flow-output table in fundamental mode.

According to the design steps of Figure 31.4, we have to derive a transition-output table from the flow- output table shown in Table 31.12, by deriving a state-output table by assigning appropriate binary numbers to states such that multiple changes do not occur for every transition from one binary number to another, possibly changing some intermediate unstable states to others. Then, if the designers want to use S-R latches, we can derive an excitation table by finding the output-input relationship of the S-R latch, as illustrated with Tables 31.7, 31.8, and 31.9. Then, we can design the loopless network inside the general model of Figure 31.3 by deriving minimal sums from the Karnaugh maps decomposed from the excitation-output table. If the designers do not want to use S-R latches, we can design the loopless network inside the general model of Figure 31.3 by deriving minimal sums from the Karnaugh maps decomposed from the transition-output table without deriving an excitation-output table.

In the case of an asynchronous sequential network, we need post-analysis of whether the designed network works reliably.

Advantages of Skew Mode

The advantages of skew-mode operation with raceless flip-flops, such as master-slave or edge-triggered flip-flops, can be summarized as follows:

1. We can use no more complex and often simpler flow-output tables (or state-output tables) in skew mode than are required in fundamental mode, making design easier (because we need not consider both unstable and stable states for each input change, and need not consider adding extra states, or changing intermediate unstable states, which are to avoid multiple changes of internal variables).

2. State assignments are greatly simplified because we need not worry about hazard due to multiple changes of internal variables. (If we want to minimize the number of gates, connections, or levels, we need to try different state assignments. This is less important than the reliable operations of the networks to be synthesized.)

3. Networks synthesized in skew mode usually require fewer internal variables than those in fundamental mode.

4. After the network synthesis, we do not need to check whether the networks contain racing hazards or not. This is probably the greatest of all the advantages of skew mode, since checking hazards and finding remedies is usually very cumbersome and time-consuming.