RF Passive IC Components:Spiral Inductors

Spiral Inductors

More than is so with capacitors, on-chip inductor options are particularly limited and unsatisfactory. Nevertheless, it is possible to build practical spiral inductors with values up to perhaps 20 nH and with Q values of approximately 10. For silicon-based RF ICs, Q degrades at high frequencies due to energy dissipation in the semiconducting substrate [8]. Additionally, noise coupling via the substrate at GHz frequencies has been reported [9]. As inductors occupy substantial chip area, they can potentially be the source and receptor of detrimental noise coupling. Furthermore, the physical phenomena underlying the substrate effects are complicated to characterize. Therefore, decoupling the inductor from the substrate can enhance the overall performance by increasing Q, improving isolation, and simplifying modeling.

Some approaches have been proposed to address the substrate issues; however, they are accompanied by drawbacks. Some [10] have suggested the use of high-resistivity (150 to 200 W-cm) silicon substrates to mimic the low-loss semi-insulating GaAs substrate, but this is rarely a practical option. Another approach selectively removes the substrate by etching a pit under the inductor [11]. However, the etch adds extra processing cost and is not readily available. Moreover, it raises reliability concerns such as packaging yield and long-term mechanical stability. For low-cost integration of inductors, the solution to substrate problems should avoid increasing process complexity.

In this section, we present the patterned ground shield (PGS) [23], which is compatible with standard silicon technologies, and which reduces the unwanted substrate effects. The great improvement provided by the PGS reduces the disparity in quality between spiral inductors made in silicon and GaAs IC technologies.

Understanding Substrate Effects

To understand why the PGS should be effective, consider first the physical model of an ordinary inductor on silicon, with one port and the substrate grounded, as shown in Figure 11.12 [8]. An on-chip inductor is physically a three-port element including the substrate. The one-port connection shown in Figure 11.12 avoids unnecessary complexity in the following discussion and at the same time preserves the inductor characteristics. In the model, the series branch consists of Ls, Rs, and Cs . Ls represents the spiral induc- tance, which can be computed using the Greenhouse method [12] or well-approximated by simple analytical formulas to be presented later. Rs is the metal series resistance whose behavior at RF is governed by the eddy current effect. This resistance accounts for the energy loss due to the skin effect in the spiral interconnect structure as well as the induced eddy current in any conductive media close to the inductor.

The series feedforward capacitance, Cs, accounts for the capacitance due to the overlaps between the spiral and the center-tap underpass [13]. The effect of the inter-turn fringing capacitance is usually small because the adjacent turns are almost at equal potentials, and therefore it is neglected in this model. The overlap capacitance is more significant because of the relatively large potential difference between the spiral and the center-tap underpass. The parasitics in the shunt branch are modeled by Cox, CSi, and RSi. Cox represents the oxide capacitance between the spiral and the substrate. The silicon substrate capacitance and resistance are modeled by CSi and RSi, respectively [14,15]. The element RSi accounts for the energy dissipation in the silicon substrate.

Expressions for the model element values are as follows:

where r is the DC resistivity of the spiral; t is the overall length of the spiral windings; w is the line width; d is the skin depth; n is the number of crossovers between the spiral and center-tap (and thus n = N – 1, where N is the number of turns); toxM1-M2 is the oxide thickness between the spiral and substrate; Csub is the substrate capacitance per unit area; and Gsub is the substrate conductance per unit area. In general, one treats Csub and Gsub as fitting parameters.

Exploration with the model reveals that the substrate loss stems primarily from the penetration of the electric field into the lossy silicon substrate. As the potential drop in the semiconductor (i.e., across RSi in Figure 11.12) increases with frequency, the energy dissipation in the substrate becomes more severe. It can be seen that increasing Rp to infinity reduces the substrate loss. It can be shown that Rp approaches infinity as RSi goes either to zero or infinity. This observation implies that Q can be improved by making the silicon substrate either a perfect insulator or a perfect conductor. Using high-resistivity silicon (or etching it away) is equivalent to making the substrate an open circuit. In the absence of the freedom to do so, the next best option is to convert the substrate into a better conductor. The approach is to insert a ground plane to block the inductor electric field from entering the silicon. In effect, this ground plane becomes a pseudo-substrate with the desired characteristics.

The ground shield cannot be a solid conductor, however, because image currents would be induced in it. These image currents tend to cancel the magnetic field of the inductor proper, decreasing the inductance. To solve this problem, the ground shield is patterned with slots orthogonal to the spiral as illustrated in Figure 11.13. The slots act as an open circuit to cut off the path of the induced loop current. The slots should be sufficiently narrow such that the vertical electric field cannot leak through the patterned ground shield into the underlying silicon substrate. With the slots etched away, the ground strips serve as the termination for the electric field. The ground strips are merged together around the four outer edges of the spiral. The separation between the merged area and the edges is not critical.

However, it is crucial that the merged area not form a closed ring around the spiral since it can potentially support unwanted loop current. The shield should be strapped with the top layer metal to provide a low- impedance path to ground. The general rule is to prevent negative mutual coupling while minimizing the impedance to ground.

The shield resistance is another critical design parameter. The purpose of the patterned ground shield is to provide a good short to ground for the electric field. Since the finite shield resistance contributes to energy loss of the inductor, it must be kept small. Specifically, by keeping the shield resistance small compared to the reactance of the oxide capacitance, the voltage drop that can develop across the shield resistance is very small. As a result, the energy loss due to the shield resistance is insignificant compared to other losses. A typical on-chip spiral inductor has parasitic oxide capacitance between 0.25 and 1 pF, depending on the size and the oxide thickness. The corresponding reactance due to the oxide capacitance at 1 to 2 GHz is of the order of 100 W, and hence a shield resistance of a few ohms is sufficiently small not to cause any noticeable loss.

With the PGS, one can expect typical improvements in Q ranging from 10 to 33%, in the frequency range of 1 to 2 GHz. Note that the inclusion of the ground shields increases Cp, which causes a fast roll- off in Q above the peak-Q frequency and a reduction in the self-resonant frequency. This modest improvement in inductor Q is certainly welcome, but is hardly spectacular by itself. However, a more dramatic improvement is evident when evaluating inductor-capacitor resonant circuits. Such LC tank circuits can absorb the parasitic capacitance of the ground shield. Since the energy stored in such parasitic elements is now part of the circuit, the overall circuit Q is greatly increased. Improvements of factors of approximately two are not unusual, so that tank circuits realized with PGS inductors possess roughly the same Q as those built in GaAs technologies.

As stated earlier, substrate noise coupling can be an issue of great concern owing to the relatively large size of typical inductors. Shielding by the PGS improves isolation by 25 dB or more at GHz frequencies. It should be noted that, as with any other isolation structure (such as a guard ring), the efficacy of the PGS is highly dependent on the integrity of the ground connection. One must often make a tradeoff between the desired isolation level and the chip area that is required to provide a low-impedance ground connection.

Simple, Accurate Expressions for Planar Spiral Inductances

In the previous section, a physically based model for planar spiral inductors was offered, and reference was made to the Greenhouse method as a means for computing the inductance value. This method uses as computational atoms the self- and mutual inductances of parallel current strips. It is relatively straightforward to apply, and yields accurate results. Nevertheless, simpler analytic formulas are generally preferred for design since important insights are usually more readily obtained.

As a specific example, square spirals are popular mainly because of their ease of layout. Other polygonal spirals have also been used to improve performance by more closely approximating a circular spiral. However, a quantitative evaluation of possible improvements is cumbersome without analytical formulas for inductance.

Among alternative shapes, hexagonal and octagonal inductors are used widely. Figures 11.14 through

11.16 and show the layout for square, hexagonal, and octagonal inductors, respectively. For a given shape, an inductor is completely specified by the number of turns n, the turn width w, the turn spacing s, and any one of the following: the outer diameter dout, the inner diameter din, the average diameter davg = 0.5(dout + din), or the fill ratio, defined as r = (dout + din)l(dout + din). The thickness of the inductor has only a very small effect on inductance and will therefore be ignored here.

We now present three approximate expressions for the inductance of square, hexagonal, and octagonal planar inductors. The first approximation is based on a modification of an expression developed by Wheeler [16]; the second is derived from electromagnetic principles by approximating the sides of the spirals as current sheets; and the third is a monomial expression derived from fitting to a large database of inductors (whose exact inductance values are obtained from a 3-D electromagnetic field solver). All three expressions are accurate, with typical errors of 2 to 3%, and very simple, and are therefore excellent candidates for use in design and optimization.

Modified Wheeler Formula

Wheeler [16] presented several formulas for planar spiral inductors, which were intended for discrete inductors. A simple modification of the original Wheeler formula allows us to obtain an expression that is valid for planar spiral integrated inductors:

where r is the fill ratio defined previously. The coefficients K1 and K2 are layout dependent and are shown in Table 11.1.

The fill factor r represents how hollow the inductor is: for small r, we have a hollow inductor (dout @ din), and for a large r we have a filled inductor (dout � din). Two inductors with the same average diameter but different fill ratios will, of course, have different inductance values; the filled one has a smaller inductance

because its inner turns are closer to the center of the spiral, and so contribute less positive mutual inductance and more negative mutual inductance. Some degree of hollowness is generally desired since the innermost turns contribute little overall inductance, but significant resistance.

Expression Based on Current Sheet Approximation

Another simple and accurate expression for the inductance of a planar spiral can be obtained by approxi- mating the sides of the spirals by symmetrical current sheets of equivalent current densities [17]. For example, in the case of the square, we obtain four identical current sheets: the current sheets on opposite sides are parallel to one another, whereas the adjacent ones are orthogonal. Using symmetry and the fact that sheets with orthogonal current sheets have zero mutual inductance, the computation of the inductance is now reduced to evaluating the self-inductance of one sheet and the mutual inductance between opposite current sheets. These self- and mutual inductances are evaluated using the concepts of geometric mean distance (GMD) and arithmetic mean distance (AMD) [17,18]. The resulting expression is:

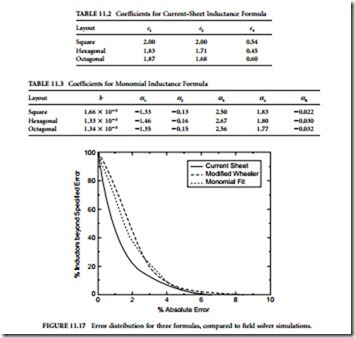
where the coefficients ci are layout dependent and are shown in Table 11.2.

A detailed derivation of these formulas can be found in Ref. 19. Since this formula is based on a current sheet approximation, its accuracy worsens as the ratio s/w becomes large. In practice, this is not a problem since practical integrated spiral inductors are built with s < w. The reason is that a smaller spacing improves the inter-winding magnetic coupling and reduces the area consumed by the spiral. A large spacing is only desired to reduce the inter-winding capacitance. This is rarely a concern as this capacitance is always dwarfed by the under-pass capacitance [8].

Data-Fitted Monomial Expression

Our final expression is based on a data-fitting technique, in which a population of thousands of inductors are simulated with an electromagnetic field solver. The inductors span the entire range of values of relevance to RF circuits. A monomial expression is then fitted to the data, which ultimately yields:

where the coefficients b and ai are layout dependent, and given in Table 11.3.

Of course, it is also possible to use other data-fitting techniques; for example, one which minimizes the maximum error of the fit, or one in which the coefficients must satisfy given in equalities or bounds. The monomial expression is useful since, like the other expressions, it is very accurate and very simple. Its real value, however, is that it can be used for the optimal design of inductors and circuits containing inductors, using geometric programming, which is a type of optimization method that requires monomial models [20,21].

Figure 11.17 shows the absolute error distributions of these expressions. The plots show that typical errors are in the 1 to 2% range, and most of the errors are below 3%. These expressions for inductance, while quite simple, are thus sufficiently accurate that field solvers are rarely necessary.

These expressions can be included in a physical, scalable lumped-circuit model for spiral inductors where, in addition to providing design insight, they allow efficient optimization schemes to be employed.