Communication-Based Design for Nanoscale SoCs:The Science of NoC Design

The Science of NoC Design

While the engineering aspects deal mostly with practical issues and implementation details, the science of NoCs perceives the network as an abstract graph with a set of rules for internode communication. This view of the network is frequently used in more theoretically oriented communities [33–37] aiming to understand the nature of complex technological, biological, and social networks.

Interestingly enough, the knowledge acquired from the science of networks can help better understand the very nature of design problems on the engineering side and guide the overall design progress. However, successful interaction between the science and engineering aspects of NoC design can be achieved only by incorporating the NoCpecific constraints into the abstract network model. For example, the behavior of the network under application-specific traffic pattern has utmost importance for efficient NoC design, while it is not necessarily a major issue for the mathematical treatment of networks. Therefore, the approaches based on these theoretical studies need to be considered and adapted in the light of such application-specific traffic patterns. More generally, the science of NoC design should have a concrete connection to the application side such that any possible outcome can be readily used by researchers working on the engineering side. This point of view is illustrated next by discussing several network properties in the context of NoC design.

Network Navigability

The performance of applications running on NoCs mainly depends on the time spent for computation and communication. While the computation time is primarily determined by the design of the IP cores

implementing the application, the communication time depends heavily on the ability of the network to move packets around in an efficient manner. Indeed, if the network enables fast and efficient packet navigation, then the communication time can be reduced significantly.

Some technological networks such as WWW, consist of more than 1 billion nodes but are clearly much easier to navigate compared to other networks (e.g., a 2D mesh) of equal size. Indeed, it is possible to reach any web page of interest with just a few clicks due to the small diameter of the WWW; as suggested recently, the longest path between any two nodes in such a network is around 19 hops [37]. For comparison, the diameter of a 2D mesh network with same number of nodes would be more than 50,000.

In general, the standard network architectures adopted from parallel computer networks [10] are only scalable in the sense that new nodes can be easily added to an already existing network, without distorting the structure and reducing the available bandwidth per node. However, the diameter (D) and the average internode distance* of a n X n 2D mesh network are proportional to n. Therefore, navigating in these networks becomes easily a major problem.

For application-specific NoCs, the detailed understanding of the communication workload can be exploited for optimization purposes [18–20]. Customized NoC topologies do not only improve the network performance, but also result in a better resource utilization. In contrast, the implementation complexity of such customized topologies, lack of standardization, etc. may represent a major handicap for the fully customized architectures. Therefore, the improvement in area and performance comes at the cost of losing the network regularity.

Fortunately, there exists a huge class of networks, commonly referred to as small-world networks [33], where one can search for network topologies with superior properties compared to standard topologies considered so far. Indeed, small-world networks are characterized by small internode distances and high clustering coefficients. Recent theoretical studies show that regular networks can be transformed into small-world net- works by introducing long-range connections between remotely located nodes [33,34]. Inspired by this idea, a good compromise between the well-structured networks and fully customized topologies can be obtained by customizing the grid-like NoC architectures with application-specific long-range links [32]. In Section 16.4, we address this very issue and show the subtle interplay between the network science and engineering aspects.

Clustering Effects

An important characteristic of the small-world networks is their dense structure which can be measured by the clustering coefficient [33]. To compute the clustering coefficient of node i (denoted by Ci), we need to focus on its neighbors. A node with ni neighbors can have at most ni(ni – 1)/2 links among them. If we denote by li the number of actual links that do exist between the neighbors, then Ci is expressed as

In other words, Ci is the ratio between the number of links that connect the neighbors of node i and the maximum number of links that can possibly exist among all its neighbors. Hence, Ci measures how tightly the neighbors of node i are connected to each other. The clustering coefficient of the network (CN) is then found by averaging the clustering coefficients over all the nodes (i.e., CN = mean(Ci)).

Implementing an application across a network requires mapping the application tasks to the network nodes. In many applications, a subset of tasks tend to communicate more frequently with each other compared to the remaining nodes. Intuitively, keeping the nodes that communicate more frequently close to each other is desirable both for performance and energy considerations. However, the nodes in the network can have only a limited number of immediate neighbors, depending on the degree of the node (i.e., the number of input/output links to the node) and other practical considerations. For this reason,

the applications can be mapped more efficiently to those network topologies where the network clustering closely follows the inherent clustering inside the application.

The clustering coefficient for most standard topologies, such as mesh networks and hypercubes, is equal to zero, because none of the immediate neighbors of any given node are directly connected to each other. For example, in Figure 16.3, the central node is connected to four immediate neighbors via solid lines. There are six possible connections (shown with dashed lines) between the four neigh- bors. However, since none of these connections does exist in reality, the clustering coefficient is zero. Similar arguments hold for the remaining nodes in a 2D network. As a result, the application-specific customization of the network topology can be also beneficial for improving the clustering of the network to match the application characteristics. Indeed, the NoC architecture customization via long- range link insertion improves the network clustering, when a long-range link of size 2, similar to the dashed lines in Figure 16.3, is inserted to the network. Hence, combined with the reduced internode distances due to the long-range links, improved clustering moves the initial topology closer to a small- world network.

Network Performance under Application-Specific Traffic Traditionally, the performance of NoCs is measured in terms of the average packet latency and maximum throughput of the network. It is possible, however, to define a unifying performance metric which provides valuable information about the average packet latency and network throughput [32]. At low traffic loads, the average packet latency exhibits a weak dependence on the traffic injection rate. However, when the traffic injection rate exceeds a critical value (λc), the packet delivery times rise abruptly and the network throughput starts to collapse (see Figure 16.4). The state of the network before congestion (i.e., the region on left-hand side of the critical value) is the congestion-free state, while the state beyond the critical value (right-hand side) is said to be the congested state. Finally, the transition from the free to the congested state is known as the phase transition region. Since larger values for λc imply higher sustainable throughput values (and the latency beyond λc increases abruptly), λc can be used as a convenient performance metric. For this reason, finding an analytical expression for λc is desirable for fast performance evaluation which can be used in an optimization loop.

Analytical Evaluation of Ac

Let us denote the total number of messages in the network, at time t, by N(t) and the aggregated packet injection rate by λ. In the free state regime (i.e., λ < λc), the network is in the steady state, so the packet injection rate equals the packet ejection rate. As a result, we can equate the injection and ejection rates

where τave is the average time each packet spends in the network, and Nave= <N(t)> the average number of packets in the network. The exact value of τave is a function of the traffic injection rate, topology, routing strategy, etc. We observe that τave shows a weak dependence on the traffic injection rate when the network is in the free state. Hence the free packet delay (τ0), which can be computed analytically, can be used to approximate τave. If we denote the average number of packets in the network, at the onset of the criticality, by N c we can write the following relation:

This approximation acts also as an upper bound for the critical load λc, since τ0 ≤ τave(τc). We note that this relation can be also found using mean field [35] and distance models [36], where N ave is approximated by the number of nodes in the network, under the assumption that the utilization of the routers is close to unity at the onset of the criticality.

The free packet delay is a function of application, as well as network topology. Therefore, a network architecture matching the communication requirements of the target application will deliver a superior performance compared to standard network topologies, such as k-ary n-cube and multistage networks [10].

Experimental Validation of Ac

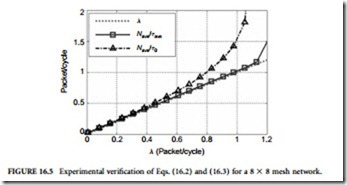
Experimental validation of Eq. (16.2) and Eq. (16.3) is shown in Figure 16.5. For reference, the dotted line shows the actual packet injection rate (λ). The solid line with square markers on it is obtained for an 8 X 8 network under the hotspot traffic,† as the ratio between the average number of packets in the network and the average packet delay at that particular injection rate.

This plot clearly shows that there is a good agreement between the actual values obtained through simulation and the ones predicted by Eq. (16.2) before entering the criticality. However, since beyond the critical traffic value the network is not anymore in a steadystate, Eq. (16.2) does not hold for higher-injection rates. The dashed line with triangular markers on it (Figure 16.5) illustrates the upper bound in Eq. (16.3). We observe that this analytical expression provides a good approximation and holds the upper bound property true.