Square wave oscillators and Op-amp square wave oscillator.

Square wave oscillators

If Fourier analysis is performed on a square wave it is found that the waveform is composed of many harmonics of the fundamental frequency. This rich harmonic content makes the square wave particularly useful as a quick test of amplifier performance. Examples of possible results are shown.

The simplest way to produce a square wave is to make a sine wave oscillator in one of the ways described earlier, then feed the output to some form of squaring circuit such as a Schmitt trigger. This is the method adopted in most commercial sine/square wave generators.

There are, however, several circuits for square wave oscillators and a description of the most common follows.

Multivibrator

Technically the multivibrator is a relaxation oscillator, working on the charging of a capacitor through a resistor. If a negative edge is applied to the circuit in (a), transistor TR 1 turns off the for time taken for the base voltage to return to 0 V. If the voltage step is the same magnitude as the supply voltage, the time that TR 1 is turned off is given by:

We now connect transistor TR 1 to another transistor through the capacitor/resistor C2R2, as shown in (b), and again apply a negative edge to capacitor C1• Transistor TR 1 again turns off for period Tl' but as T1 ends, the negative edge turns TR2 off in a similar manner, for time T2 given by:

If the output of transistor TR2 is now connected back to capacitor C1

as shown in (c), when transistorTR 2 turns back on the negative edge turns transistor TR 1 off again, repeating the cycle. The circuit continues to oscillate, giving complementary square waves from transistors TR 1 and TR2• The circuit is usually drawn similar to the circuit in (d).

It can be a problem deciding how a multivibrator actually starts (and it should be said that they sometimes do not!). Starting is usually brought about by differences in the transistor gains at first tum-on. When a multivibrator does not start, both transistors end up turned on, with base current provided through the base resistors. This can be avoided by deliberately having an asymmetrical waveform with T1 and T2 different values.

Because of its simplicity, the multivibrator has many shortcom­ ings. The major problem is the poor positive edge. The collector resistors are loaded by the timing capacitors, giving a marked exponential shape to the waveform.

The other problem is that the bases of the transistors are taken negative to a voltage equivalent to the supply. Most transistors have a maximum reverse Vbe of about 5 V, implying that the simple circuit can only be used on 5 V supplies. In practice, higher supplies can be used, but the transistor base emitter junction acts as a zener, limiting the base to around 6 V negative. This does not appear to harm the transistor, but causes the actual frequency to differ widely from the theoretical value.

Op-amp square wave oscillator

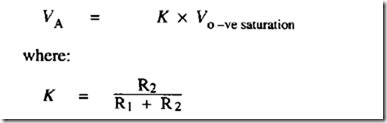
The circuit shown is a useful oscillator where a large voltage swing is required. Referring to the timing diagram, at time t = 0 the amplifier is in negative saturation and:

Point B charges towards the negative supply rail via the timing resistor R. When points B and A are the same voltage, V switches to positive saturation. Point A is now at:

and point B charges towards the positive rail. When points B and A are at the same voltage, Vo switches back to negative saturation, recommencing the sequence.

The output thus oscillates between V+ve and V-ve, point A between KV+ve and KV-ve, and point B rises and falls exponentially between the same voltages as point A.

Blocking oscillator

At first sight the blocking oscillator might be mistaken for the LC oscillator described earlier. Operation is, however, completely different. A typical blocking oscillator circuit is shown. The oscillatory sequence starts with the timing capacitor, C, charged

negative and transistor TR 1 turned off. Timing resistor, R, charges C and the base voltage starts to rise towards Vee· At about 0.5 V, transistor TR 1 turns on, and current flows through the primary of the transformer. This couples back into the base, causing more current to flow. Regenerative action takes place, and the increased base current flows through capacitor C, driving the RC junction quickly negative, cutting transistor TR 1 off. The sequence now starts again.

The output consists of short negative pulses (with width determined by the transistor and transformer) occurring at regular intervals (with time determined by RC).

Integrated circuit astables for digital circuits

Control circuits using TTL and CMOS logic gates frequently require oscillator circuits to act as system clocks. These can easily be implemented using specially designed integrated circuits. A typical example is the 555 timer chip shown in (a).

This consists of a memory flip-flop, and two comparators set at two-thirds and one-third of Vee·

To construct an astable we add two resistors and a capacitor, as shown in (b). Assume that the memory has been set, and the voltage on the capacitor is approximately 1/2 Vee· The capacitor charges through resistors R 1 and R2•

When the voltage reaches 2/3 Vee• comparator I resets the memory. The capacitor now discharges via resistor R2 to pin 7. When the voltage reaches 1/3 Vee• comparator 2 sets the memory and the sequence starts again.

Oscillators for use with digital circuits need fast falling and rising edges if problems are not to be encountered with noise. Counter circuits, in particular, are prone to double counts on slow edges. Oscillator circuits with very fast edges can be built using Schmitt trigger gates, and a circuit for a gated CMOS oscillator is shown.

Digital circuits

Many control schemes rely on decisions that can only be in one of two states. A contact can be open or closed, for example, or a gas flame lit or not lit.

The electronic version of this type of circuit is known as a digital circuit, and signals inside digital circuits can only be at one or other of two voltages. These two voltages are usually referred to as a 'I' or a '0'. In TTL integrated digital circuits, for example, a I is represented by 3.5 V and a 0 by 0 V.

Digital circuits can be classified into two main groups. The first group is concerned with control of objects (e.g. start drill, advance chuck-head at low pressure until limit switch A makes, open high pressure valve, advance until limit switch B makes, then retract at high speed). The second group is concerned with numbers, and digital circuits are used for arithmetic and counting purposes.

Basic logic gates

It is convenient to compare many of the basic logic gates with relay circuits.

AND gate

The first gate is the AND gate. This is represented by the symbol in (a), and is equivalent to the relay circuit in (b).

The output C is at I if, and only if, both inputs A and B are at I.

Otherwise the output is 0. A so-called truth table, listing all possible input combinations, is given in (c).

OR gate

The second gate is an OR gate, shown in (a). Output C is 1 if ANY input is It is thus similar in operation to the relay scheme in (b), and its truth table is shown in (c).

Although the AND and OR gates are shown here with just two inputs, they can have any number of inputs. An 8-input AND gate, for example, will have its output at 1 if, and only if, all 8 inputs are also 1.

Inverter

The inverter has one input and one output and is shown in (a). The output is the opposite state to the input; 1 in gives 0 out and vice versa. This is similar to the normally closed contact in (b).

Where possible, logic designers build logic schemes around the next two gates described. Of all the gates these are probably the most versatile.

NAND gate

The NAND gate shown in (a) is simply an AND gate followed by an inverter, as redrawn in (b). The output is thus 0 when all inputs are 1.

NOR gate

The NOR gate shown in (a) is an OR gate followed by an inverter. The output is 0 when any input is 1.

Exclusive OR gate

The exclusive OR gate (XOR for short) is not particularly common. It has only two inputs, and checks for these being the same (i.e. both 1 or both 0).

The gate is shown in (a), with its truth table in (b). There is no simple relay equivalent to a XOR gate.