Hartley oscillator and Phase-shift oscillators.
Hartley oscillator
The Hartley oscillator uses a centre-tapped coil. A typical arrange ment is shown. The tuned circuit consists of capacitor C and two coil sections L3 and Lb. Capacitor C1 is again a coupling capacitor.
The resonant frequency is given by:
Values of inductance and capacitance become prohibitively large at frequencies much below 50 kHz, and this really limits the use of LC oscillators to RF applications. Fortunately for the circuit designer, however, phase shift oscillator circuits are well suited to frequencies below 50 kHz.
Phase-shift oscillators
Phase-shift oscillators consist of an amplifier with feedback incorporating a deliberate phase shift. At one specific frequency the total phase shift is some multiple of 360 degrees and if loop gain is greater than unity, then oscillations occur.
Phase shift is usually introduced using RC networks, allowingcheap components to be used. At frequencies above about 100kHz, stray capacitance becomes a problem and it becomes easier to use LC oscillators described earlier.
Three-stage RC filter oscillator
A single common emitter transistor oscillator has, effectively, a phase shift of 180 degrees at all frequencies from base to collector. If the collector is connected back to the base by a network having a phase shift of 180 degrees, total phase shift is 360 degrees and oscillation occurs.
The three-stage filter in (a) is arranged such that each stage has a phase shift of 60 degrees, and thus a total phase shift of 180 degrees. For each stage the required 60 degrees phase shift occurs at a frequency:
In a series of stages the reactance is modified by succeeding stages, and for three stages 180 degree phase shift occurs at:
A practical phase-shift oscillator is shown in (b). Resistors Rbl• Rb2 and Rin of the transistor, all in parallel, form the third resistor. As the input resistance of the transistor is subject to wide variation, it is common for the actual oscillation frequency to be different from the theoretical frequency.
The three-stage filter attenuates the signal from collector to base, but this is more than compensated for by the voltage gain of the transistor. Amplitude of the output is again limited by the transistor coming out of conduction or going into saturation. Some distortion of the output waveform therefore occurs.
Wien bridge oscillators
The Wien bridge is an AC version of the well-known Wheatstone bridge, and is shown in its basic form. If analysed by AC theory, it is found to balance at a frequency of:
and at balance the output voltage is in phase with the input voltage (but one-third of the amplitude).
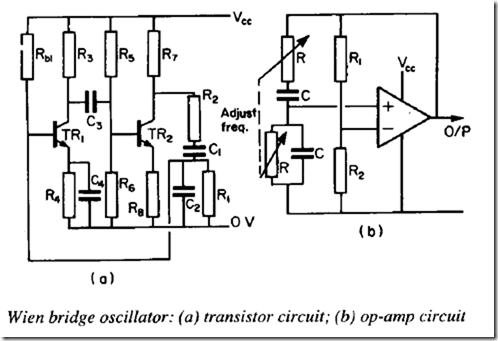
Phase shift at balance is zero, so the Wien bridge has to be used with a non-inverting amplifier if oscillation is to occur. This can be done either by using a two-stage transistor amplifier, as shown in (a), or an integrated circuit operational amplifier, as in (b). Other circuit components may modify the balance condition, and in (a), R 1 has to be chosen to take account of the parallel resistance of Rbl, and Rin of transistor TR 1•
One advantage of the Wien bridge oscillator is the simplicity of tuning. This can be achieved by a means of a two-track (double ganged) potentiometer.
Amplitude is limited by events similar to those described for earlier oscillators. IfR 1 in (b) is replaced by a thermistor, however, amplitude can be made reasonably constant. If oscillation amplitude increases, temperature of the thermistor increases and its resistance reduces. This increases negative feedback and reduces amplifier gain. The circuit stabilises at the correct gain to just maintain oscillation (i.e. open-loop gain is unity).
Crystal oscillators
All the oscillators so far described have one major shortcoming; their frequency is dependent on circuit characteristics outside the direct control of the designer. Outside events such as temperature and supply variations cause the frequency of oscillation to vary from day to day.
In many applications a precise frequency is not important, but there are several circuits where accuracy is important. A UHF mobile radio, for example, working on 460 MHz has to keep its carrier constant to a few kilohertz despite temperature changes, varying battery voltages and mechanical vibration.
Oscillators designed to these tight specifications use the properties of quartz crystals. These crystals are capable of vibrating up to high frequencies, and as they do so the piezoelectric effect develops an alternating voltage across the two opposite faces. The crystal then behaves as a tuned circuit having a very high L/C ratio and very high Q.
Typical crystal oscillators are shown in (a) and (b). Coupling capacitor C1 in (b) is sometimes implemented by the transistor collector/base capacitance.
The highest natural frequency it is possible to attain easily with a crystal is of the order of I MHz. For frequencies above this, it is usual to drive the crystal at a harmonic frequency, the choice of harmonic being determined by some external LC circuit such as the collector load in (a).
A very limited amount of tuning can be done by shunting the crystal with a low value capacitor. The range available is less than 0.01%, so tuning can only be a fine trim. Once set, frequency stability is excellent and stabilities of I part in 108 are easily obtained. If care is taken, and the circuit kept in a temperature controlled environment, stabilities better than 1 part in 1010 are attainable.



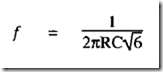







Comments
Post a Comment