Arithmetic and computing circuits and Encoders and decoders.

Arithmetic and computing circuits

Human beings count to a base of ten. This means that each digit in a decimal number represents a power of ten. The number 74057, for example, means:

The reason we count to a base of ten is, of course, because we have ten fingers. Number systems can be constructed to any base; there is nothing magic about ten. If we had twelve fingers we would probably have counted to a base of twelve.

Of particular interest in electronics and computing is the number system to a base of two, called binary. In binary, each digit represents a power of two (I, 2, 4, 8, 16, 32 and so on). Each digit is called a bit. Using the same approach as we did for the decimal number above we can therefore evaluate a binary number, 11010 say, as:

The binary number 11010 is therefore decimal 26.

A more complex example, 1101110I, noting that 2 x 2 = 4, and 2 x 2 x 2 = 8 and so on:

The binary number 11011101 is thus decimal221.

Any decimal number can be represented as an equivalent binary number, but the resulting binary representation is confusing for human beings. Binary is, however, ideal for digital circuits as a number can be represented as a combination of on/off states.

Conversion from binary to decimal is done by repeated division by two and noting the remainders (which will be 0 or I). This is best shown by example. To convert decimal 23:

Decimal23 is therefore binary lOIII. The technique can be used for any size of decimal number.

In computing, the engineer often has to deal with binary numbers and these are difficult to interpret directly. Number systems based on 16 (called hex) and 8 (called octal) are a useful halfway house between binary and decimal.

Hex uses letters A, B, C, D, E, F to cover the decimal numbers 10 to 15 (Dis decimal 13 for example). Octal omits numerals 8 and 9. The counting sequence is thus:

The convenience of hex and octal is that conversion to and from binary is simple because a hex number is represented by four binary bits, and an octal number by three binary bits. For example, the number 10110101 can be represented in hex as:

The hex representation B5 and the octal representation 265 are found much easier than conversion to decimal (to give 181). Hex representation is common in computing.

Encoders and decoders

These devices convert between decimal and binary for interfacing to decimal devices such as thumbwheel switches and decade displays. An encoder converts ten decimal input lines to 4-bit binary, and a decoder converts 4-bit binary to ten decimal output lines, as shown on the logic symbols in (a) and (c) over.

Construction of encoders and decoders is a simple, if somewhat lengthy, combinational logic design problem. A part of an encoder (for the bit representing 2) and a decoder (for the decimal output 7) are shown in (b) and (d).

Counters

A binary counter will count pulses at its input. A four-bit counter output will thus go:

It's clear from this that a bit changes from 0 to 1 or 1 to 0 each time its predecessor goes from 1 to a 0.

If negative edge-triggered D-types are connected, as in (a), they behave as counters. Counters can also be implemented using JK flip­ flop, with J = K = 1.

An up-counter, known as this for obvious reasons, is shown in (a). If the coupling between stages is taken from the Qpins as in (b),

with the output still being taken from the Q pins, the counter counts down. This arrangement is known as a down-counter. By selecting the interstage coupling a bidirectional counter can be constructed.

Synchronous counters

The counters already described are called ripple-through or non­ synchronous counters because the change of state of the counter ripples through from the least significant end and the counter outputs do not change simultaneously. In slow applications this is of little import, but at high speeds the time taken to go, say, from 0 1111111  to 11111111 can be significant. Problems can also arise if the counter outputs are being decoded, as false glitches can appear on the decoder outputs while the count change ripples through.

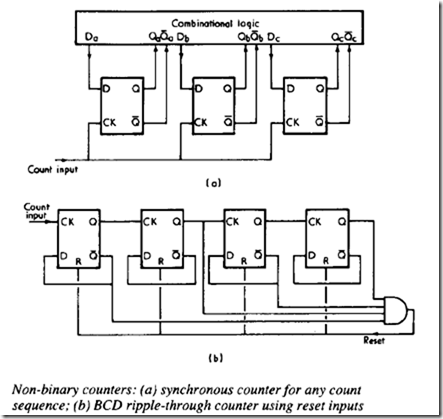
These problems can be overcome by constructing a synchronous counter circuit, a JK form of which is shown below. This uses combinational logic to look at preceding stages and set the JK inputs to I if a toggle is required. With this arrangement, all counter outputs change together and the counter can be safely decoded.

Counters to non-binary bases

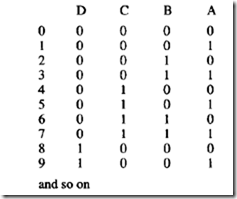
Counters are often required to give non-binary counts. A BCD counter, for example, omits the counts for 10, II, 12, 13, 14, 15. Such counters can be designed around state diagrams.

General principle is shown in (a). The Q and Q outputs from the counter flip-flops are fed to a combinational logic circuit which sets up the correct D-input levels for the next counter state. This sort of technique inherently gives a synchronous counter circuit.

This technique can be used to design any count sequence, however odd, with D-type and JK flip-flops.

If the required count sequence is a truncated binary count, on the other hand, it is often simpler to force a reset or set of individual bits at the required point.

A circuit for a BCD counter is shown in (b), where a single gate detects a count often (1010) and forces a counter rese.t.

Arithmetic units

The first arithmetic unit we need is an adder. This is shown diagrammatically and is constructed using multiple identical blocks, each block adding one bit. The block is called a one-bit adder. It has three inputs, the A and B number inputs and the carry in from the previous stage. It has two outputs, the bit sum and the carry out to the next stage.

Subtraction is done by a specialised form of addition. Suppose we are adding two numbers in decimal, but we can only represent numbers up to 999. We add:

The highest I, representing 1000, is lost leaving us with 41. The number 994 thus looks like -6, and is called the complement of 6.

Similar methods are used to subtract binary numbers. This is known as two's complement arithmetic.

The formation of a two's complement is achieved by inverting each bit and adding I. To form the two's complement of 5 to a length of 5 bits, for example:

It is usual to represent the sign by the most significant bit; I denotes a negative number, 0 a positive number.

It might be thought that the next blocks we need are multiply and divide. In fact, multiplier and divider logic blocks are practically unknown, these functions being easier to implement by computer. The shift register circuit following does limited multiplication and division by two.

Shift register

A shift register moves a binary number by one column for each input pulse. It can be designed to shift to the left or to the right. Shifting to the left (shift up) multiplies by two, whereas shifting to the right (shift down) divides by two: