Oscillators and LC circuits.
Oscillators
An oscillator is an electronic circuit which converts power from a DC supply into alternating power. Basically, oscillators fall into three classes: sine wave, square wave and other waveforms.
The conditions for maintaining oscillations are that loop gain is equal to (or greater than) unity, and feedback exists with a loop phase shift of zero (or some multiple of 360 degrees) at the oscillator frequency.
Sine wave oscillators can be constructed using the resonant properties of an LC circuit, deliberately using an RC network to induce phase shift around an amplifier, or by using the piezoelectric effects of a quartz crystal. These methods allow sine wave oscillators to be built from frequencies below 0.1 Hz to frequencies over 400MHz.
LC circuits
The resonant properties of LC circuits can easily be calculated from AC theory. Two arrangements are possible. The series arrangement over exhibits a minimum impedance at resonance, as the inductive and capacitive reactances are equal at the resonant frequency, but have opposite phase effects and hence cancel. Resonance therefore occurs when:
The series resonant circuit is sometimes called an acceptor circuit.
The parallel arrangement over is more widely used in oscillators. This exhibits maximum impedance at resonance, and the resonant frequency is again given by:
The output voltage therefore holds the highest value of Vi. If the diode is reversed the output voltage is the lowest value of Vi. A sample and hold circuit can be formed by replacing the diode with a switch (either a physical contact or a CMOS transmission gate).
Voltage V now holds the value of V at the instant the switch was last opened. Sample and hold circuits are used to freeze the value of an input to a digital-to-analog converter.
Oscillators
An oscillator is an electronic circuit which converts power from a DC supply into alternating power. Basically, oscillators fall into three classes: sine wave, square wave and other waveforms.
The conditions for maintaining oscillations are that loop gain is equal to (or greater than) unity, and feedback exists with a loop phase shift of zero (or some multiple of 360 degrees) at the oscillator frequency.
Sine wave oscillators can be constructed using the resonant properties of an LC circuit, deliberately using an RC network to induce phase shift around an amplifier, or by using the piezoelectric effects of a quartz crystal. These methods allow sine wave oscillators to be built from frequencies below 0.1 Hz to frequencies over 400MHz.
LC circuits
The resonant properties of LC circuits can easily be calculated from AC theory. Two arrangements are possible. The series arrangement over exhibits a minimum impedance at resonance, as the inductive and capacitive reactances are equal at the resonant frequency, but have opposite phase effects and hence cancel. Resonance therefore occurs when:
The series resonant circuit is sometimes called an acceptor circuit.
The parallel arrangement over is more widely used in oscillators. This exhibits maximum impedance at resonance, and the resonant frequency is again given by:
The simplest form of LC oscillator is the arrangement shown. The tuned circuit is connected in the collector and feedback to the base is provided by Rbl' Rb2 and Re.
Once oscillations start, the amplitude increases until transistor TR 1 either comes out of conduction on the positive cycle, or bottoms on the negative cycle. Under either of these conditions the loop gain (over a full cycle) is unity. It follows that there is slight distortion on the peaks of the output waveform. This is normally unimportant.
Transformers are quite expensive to manufacture, and it is difficult to wind them with the degree of precision required for some oscillator applications. Oscillator circuits have evolved, therefore, using simple coils, and most are variations on the Colpitts and Hartley oscillators described below.
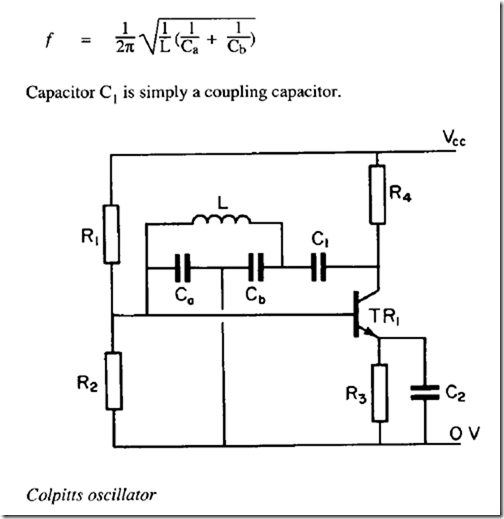
Colpitts oscillator
The resonant components in a Colpitts oscillator consist of a coil and two capacitors in series. A typical Colpitts oscillator is shown. The tuned circuit consists of coil L and capacitors c•. Cb. The resonant frequency is given by:
Normally capacitor Ca is chosen such that its reactance is small at resonance, ensuring that the transistor input impedance does not load the circuit. This means that Ca >> Cb; hence to a first approximation:

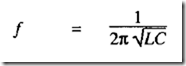








Comments
Post a Comment