Feedback Amplifiers part4

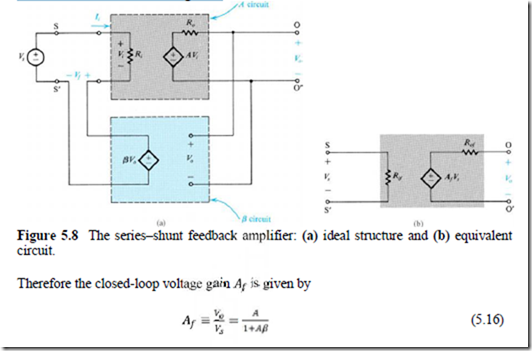
THE SERIES-SHUNT FEEDBACK AMPLIFIER

The Ideal Situation

It consists of a unilateral open-loop amplifier (the A circuit) and an ideal voltagemixing voltage-sampling feedback network (the β circuit). The A circuit has an input resisiance , a voltage gain A, and an output resistance . It is assumed that the source and load resistances have been included inside the A circuit. Furthermore, note that the circuit does not load the A circuit; that is, connecting the β circuit does not change the value of A (defined as ≡ ⁄ ).The circuit of Fig. 5.8(a) exactly follows the ideal feedback model of Fig. 5.1.

Note that A and β have reciprocal units. This in fact is always the case, resulting in a dimensionless loop gain . The equivalent circuit model of the series-shunt feedback amplifier is shown in Fig. 5.8(b). Here and denote the input and output resistances with feedback. The relationship between and can be established by considering the circuit in Fig.

That is, in this case the negative feedback increases the input resistance by a factor equal to the amount of feedback. Since the derivation above does not depend on the method of sampling (shunt or series), it follows that the relationship between and is a function only of the method of mixing. Note, however, that this result is not surprising and is physically intuitive: Since the feedback voltage subtracts from , , the voltage that appears across ,that is, [ = ⁄(1 + )] becomes quite small. Thus the input current becomes correspondingly small and the resistance seen by , becomes large. To find the output resistance, of the feedback amplifier in Fig. 5.8(a), we reduce to zero and apply a test voltage at the output, as shown in Fig. 5.9.

That is, the negative feedback in this case reduces the output resistance by a factor equal to the amount of feedback. With a little thought one can see that the derivation of Eq. (5.19) depends only on the method of sampling. Again, this result is not surprising and is physically intuitive: Since the feedback samples the output voltage , , it acts to stabilize the value of ,that is, to reduce changes in the value of ,, including changes that might be brought about by changing the current drawn from the amplifier output terminals. This, in effect, means that voltage-sampling feedback reduces the output resistance.

The Practical Situation

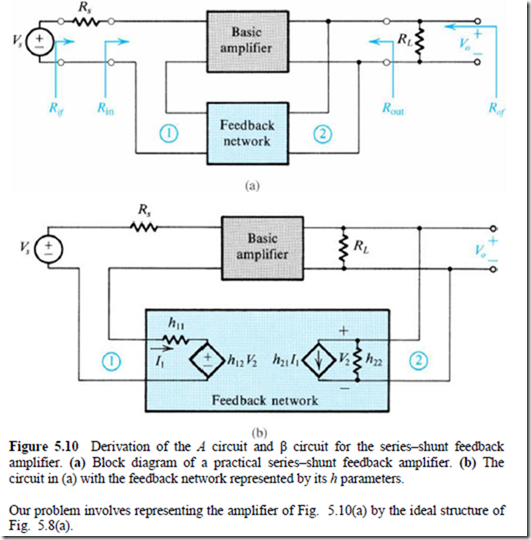
In a practical series-shunt feedback amplifier, t ba twork will not be an ideal voltage-controlled voltage source, but is us si and hence will load the basic amplifier and thus affect the values of d In addition, the source and load resistances will affect these three para e problem is as follows: Given a series-shunt feedback amplifier represented by the block diagram of Fig. 5.10(a), find the A circuit and the β circuit.

1. As a first step toward that end, the source and load resistances should be lumped with the basic amplifier.

2. Represent the two-port feedback network in terms of its h parameters as illustrated in Fig. 5.10(b). The choice of h parameters is based on the fact that this is the only parameter set that represents the feedback network by a series network at port 1 and a parallel network at port 2. Such a representation is convenient in view of the series connection at the input and the parallel connection at the output.

3. Examination of the circuit in Fig.5.10(b) reveals that the current source ℎ represents the forward transmission of the feedback network. Since the feedback network is usually passive, its forward transmission can be neglected in comparison to the much larger forward transmission of the basic amplifier. We will therefore assume that |ℎ | ≪ |ℎ | and thus omit the controlled source ℎ altogether.

4. Compare the circuit of Fig. 5.10(b) (after eliminating the current source ℎ ) with the ideal circuit of Fig. 5.8(a). We see that by including ℎ and ℎ with the basic amplifier we obtain the circuit shown in Fig. 5.10(c), which is very similar to the ideal circuit. Now, if the basic amplifier is unilateral, a situation that prevails when |ℎ | ≪ |ℎ | then the circuit of Fig.5.10(c) is equivalent to the ideal circuit.

5. It follows then that the A circuit is obtained by augmenting the basic amplifier at the input with the source impedance and the impedance ℎ of the feedback network, and at the output with the load impedance and the admittance ℎ of the feedback network.

6. Hence the loading effect of the feedback network on the basic amplifier is represented by the components ℎ and ℎ . From the definitions of the h parameters we see that ℎ is the impedance looking into port 1 of the feedback network with port 2 short-circuited. Since port 2 of the feedback network is connected in shunt with the output port of the amplifier, short-circuiting port 2 destroys the feedback. Similarly, ℎ is the admittance looking into port 2 of the feedback network with port 1 open-circuited. Since port 1 of the feedback network is connected in series with the amplifier input, open-circuiting port 1 destroys the feedback. These observations suggest a simple rule for finding the loading effects of the feedback network on the basic amplifier: The loading effect is found by looking into the appropriate port of the feedback network while the other port is opencircuited or short-circuited so as to destroy the feedback. If the connection is a shunt one, we short-circuit the port; if it is a series one, we open-circuit it. This simple rule applies also to the other three feedback topologies.

Thus to measure β one applies a voltage to port 2 of the feedback network and measures the voltage that appears at port 1, while the latter port is open-circuited.

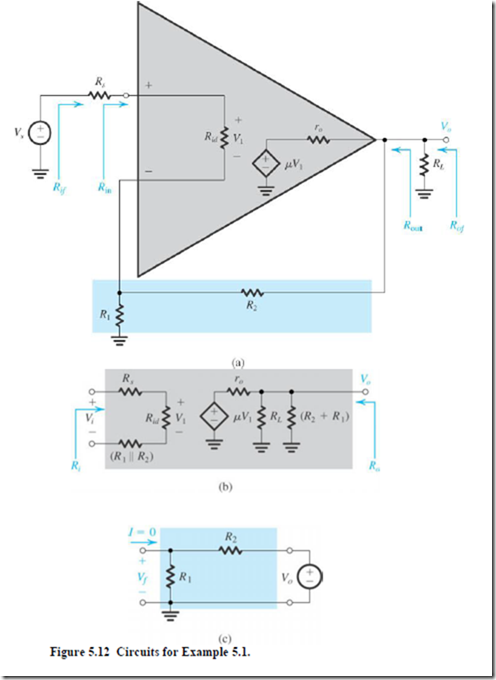
Exercise 1: Figure 5.12(a) shows an op amp connected in the noninverting configuration. The op amp has an open-loop gain μ, a differential input resistance , aud an output resistance . Recall that in our analysis of op-amp circuits in Chapter 2, we neglected the effects of (assumed it to be infinite) and of (assumed it to be zero). Here we wish to use the feedback method to analyze the circuit taking both and into account. Find expressions for A, β , the closed-loop gain ⁄ , the input resistance (see Fig. 5.12a), and the output resistance . Also find numerical values, given μ=104, = 100

Solution
Feedback network includes R1 and R2.Output voltage is sampled in shunt and feedback voltage is mixed in series with the input.
The A circuit is obtained following the rules of Fig. 5.11 and is shown in Fig. 5.12(b).
Now, by inspection we get,

DETERMINING THE LOOP GAIN

We have already seen that the loop gain Aβ is a very important quantity that characterizes a feedback loop. Furthermore, it will be shown that Aβ determines whether the feedback amplifier is stable (as opposed to oscillatory). In this section, we shall describe an alternative approach to the determination of loop gain.

Consider first the general feedback amplifier shown in Fig. 5.1. Let the external source , be set to zero. Open the feedback loop by breaking the connection of to the feedback network and apply a test signal . We see that the signal at the output of the feedback network is = ; that at the input of the basic amplifier is = − ; and the signal at the output of the amplifier, where the loop was broken, will be = − . It follows that the loop gain is given by the negative of the ratio of the returned signal to the applied test signal; that is, = − ⁄ . It should also be obvious that this applies regardless of where the loop is broken. However, in breaking the feedback loop of a practical amplifier circuit, we must ensure that the conditions that existed prior to breaking the loop do not change. This is achieved by terminating the loop where it is opened with an impedance equal to that seen before the loop was broken. Consider the conceptual feedback loop shown in Fig. 5.13(a). If we break the loop at XX', and apply a test voltage Vt, to the terminals thus created to the left of XX', the terminals at the right of XX' should be loaded with an impedance Zt, as shown in Fig. 5.13(b). The impedance Zt, is equal to that previously seen looking to the left of XX'. The loop gain Aβ is then determined from

Note: In some cases it may be convenient to determine by applying a test current and finding the returned current signal . In this case, = − / . An alternative equivalent method for determining Aβ (see Rosenstark, 1986) that is usually convenient to employ especially in SPICE simulations is as follows: As before, the loop is broken at a convenient point. Then the open-circuit transfer function is determined as indicated in Fig. 5.13(c), and the short-circuit transfer function is determined as shown in Fig. 5.13(d). These two transfer functions are then combined to obtain the loop gain Aβ,

This method is particularly useful when it is not easy to determine the termination impedance . To illustrate the process of determining loop gain, we consider the feedback loop shown in Fig. 5.14(a). This feedback loop represents both the inverting and the noninverting opamp configurations. Using a simple equivalent circuit model for the op amp we obtain the circuit of Fig, 5.14(b). Examination of this circuit reveals that a convenient place to break the loop is at the input terminals of the op amp. The loop, broken in this manner, is shown in Fig. 5.14(c) with a test signal , applied to the right-hand-side terminals and a resistance terminating the left-hand-side terminals. The returned voltage is found by inspection as