Differential Amplifiers and Multistage Amplifiers part3
FREQUENCY RESPONSE OF THE DIFFERENTIAL AMPLIFIER
In this section we study the frequency response of the differential amplifier. We will con-sider the variation with frequency of both the differential gain and the common-mode gain and hence of the CMRR. Also, we consider MOS circuits only; the bipolar case is a straightforward extension.
Analysis of the Resistively Loaded MOS Amplifier
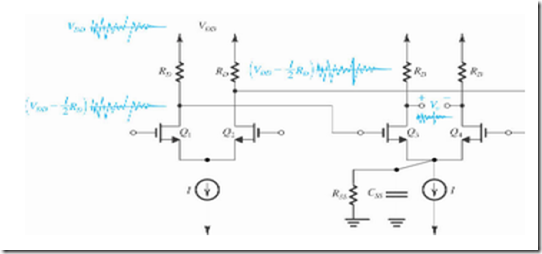
The basic, resistively loaded MOS differential pair is shown in Fig.32(a). Note that we have explicitly shown the transistor Qs that supplies the bias current I. We observe a dc bias voltage VBIAS at its gate, usually Qs is part of a current mirror. Most importantly, we are interested in the total impedance between node 5 and ground, Zss. As we shall shortly see, this impedance plays a significant role in determining the common-mode gain and the CMRR of the differential amplifier. Resistance Rss is simply the output resistance of current source Qs. Capacitance Css is the total capacitance between node S and ground and includes Cdb and Cgd of Qs, as well as Csbl, and Csb2, This capacitance can be significant, especially if wide transistors are used for Qs, Q1, and Q2.
The differential half-circuit shown in Fig.32(b) can be used to determine the frequency dependence of the differential gain Vo/ Vid. The gain function Ad(s) of the differential amplifier will be identical to the transfer function of this common-source
amplifier. The frequency response of the common-source amplifier was covered in great detail in previous chapter.
FIG32 (a) A resistively loaded MOS differential pair with the transistor supplying the bias current explicitly shown. It is assumed that the total impedance between node S and ground, Zss consists of a resistance Rss in parallel with a capacitance Css (b) Differ-ential half-circuit (c) Common- mode half-circuit.
The common-mode half-circuit is shown in Fig. 8.32(c). Although this circuit has other capacitances, namely CgS, Cgd and Cdb of the transistor in addition to other stray capaci-tances. we have chosen to show only Css/2. This is because (Css/2) together with (2Rss) forms a real-axis zero in the common- mode gain function at a frequency much lower than those of the other poles and zeros of the circuit. This zero then dominates the frequency dependence of Acm and CMRR.
If the output of the differential amplifier is taken single-endedly, then the common-mode gain of interest is Vocm/Vicm. More typically, the output is taken differentially. Nevertheless, VoCm/Vicm still plays a major role in determining
the common-mode gain. To be specific, consider what happens when the output is taken differentially and there is a mismatch ΔRD between the two drain resistances. The resulting common-mode gain was found to be eqn (49),
which is simply the product of Vocm/Vlcm (single ended) and the per-unit mismatch (ΔRD/RD). Similar expressions can be found for the effects of other circuit mismatches. The important point to note is that the factor RD/(2Rss) is always present in these expressions. Thus, the frequency dependence of Acm can be obtained by replacing Rss by Zss in this factor. This leads to
from which we see that Acm acquires a zero on the negative real-axis of the s- plane with frequency wz

Although we considered only the common-mode gain resulting from an RD mismatch, it should be obvious that the results apply to the common-mode gain resulting from any other mismatch. For instance, it applies equally well to the case of a gm mismatch modifying Eq.63 by replacing Rss by Zss, and so on.
Before leaving this section, it is interesting to point out an important trade-off found in the design of the current-source transistor Qs: In order to operate this current source with a small VDS (to conserve the already low VDD), we desire to operate the transistor at a low overdrive voltage Vov. For a given value of the current I. This means using a large W/L ratio (i.e.. a wide transistor). This in turn increases Css and hence lowers fz with the result that the CMRR deteriorates (i.e., decreases) at a relatively low frequency. Thus there is a
FIGURE33 Variation of (a) common-mode gain (b) differential gain and (c) common-mode rejection ratio with frequency.
trade-off between the need to reduce the dc voltage across Qs and the need to keep the CMRR reasonably high at higher frequencies.
To appreciate the need for high CMRR at higher frequencies, consider the situation illustrated in Fig. 34: We show two stages of a differential amplifier whose power-supply voltage VDD is corrupted with high-frequency noise.
Since the quiescent voltage at each of the drains of Q1 and Q2 is [VDD - (l/2) RD], we see that vDI and vD2 will have the same high-
FIG.34 The second stage in a differential amplifier is relied on lo suppress high-frequency noise injected by the power supply of the first stage, and therefore must maintain a high CMRR at higher frequen-cies-
frequency noise as VDD. This high-frequency noise then constitutes a common-mode input signal to the second differential stage, formed by Q3 and Q4. If the second differential stage is perfectly matched, its differential output voltage Vo should be free of high-frequency noise. However, in practice there is no such thing as perfect matching and the second stage will have a finite common-mode gain. Furthermore, because of the zero formed by Rss and Css of the second stage, the common-mode gain will increase with frequency, causing some of the noise to make its way to Vo With careful design, this undesirable component of Vo can be kept small.
Analysis of the Active-Loaded MOS Amplifier
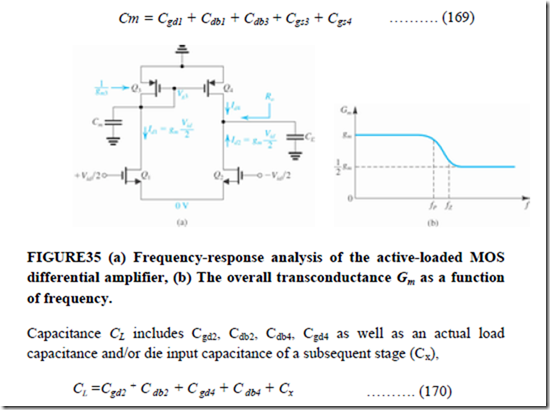
We now consider the frequency response of the current-mirror-loaded MOS differential-pair circuit. The circuit is shown in Fig35(a) with two capacitances indicated: Cm, which is the total capacitance at the input node of the current mirror, and CL which is the total capacitance at the output node. Capacitance Cm is mainly formed by Cgs3 and C gs4 but also includes Cgd1, Cdb1, and C db3
FIGURE35 (a) Frequency-response analysis of the active-loaded MOS differential amplifier, (b) The overall transconductance Gm as a function of frequency.
Capacitance CL includes Cgd2, Cdb2, Cdb4, Cgd4 as well as an actual load capacitance and/or die input capacitance of a subsequent stage (Cx),
These two capacitances primarily determine the dependence of the differential gain of this amplifier on frequency.
As indicated in Fig.34(a) the input differential signal vld is applied in a balanced fashion. Transistor Q1 will conduct a drain current signal of gm vid/ 2, which flows through the diode-connected transistor Q3 and thus through the parallel combination of (1 /gm3) and Cm where we have neglected the resistances ro1 and r03 which are much larger than (1 / gm3). Thus
We recognize the first factor on the right-hand side as the dc gain of the amplifier. The second factor indicates that CL and Ro form a pole with frequency fP1.
This, of course, is an entirely expected result, and in fact this output pole is often dominant, especially when a large load capacitance is present. The third factor on the right-hand side of Eq. (177) indicates that the capacitance Cm at the input of the current mirror gives rise to a pole with frequency fP2
Where fT is the frequency at which the magnitude of the high-frequency current gain of the MOSFET becomes unity. Thus, the mirror pole and zero occur at very high frequencies. Nevertheless, their effect can be significant.
It is interesting and useful to observe that the path of the signal current produced by Q1 has a transfer function different from that of the signal current produced by Q2. It is the first signal that encounters Cm and experiences the mirror pole. This observation leads to an interesting view of the effect of
Cm on the overall transconductance Gm of the differential amplifier: As we learnt earlier, at low frequencies Idl is replicated by the mirror Q3 – Q4 in the collector of Q4 as Id4,which adds to Id2 to provide a factor-of-2 increase in Gm (thus making Gm equal to gm which is double the value available without the current mirror). Now, at high frequen-cies Cm acts as a short circuit causing Vg3 to be zero and hence id4 will be zero, reducing Gm to gm/2. Thus, if the output is short-circuited to ground and the short-circuit transconductance Gm is plotted versus frequency, the plot will have the shape shown in Fig.35(b).
EXAMPLE
Consider an active-loaded MOS differential amplifier of the type shown in Fig. 28(a). Assume that for all transistors, W/L = 8.µm/0.36 µm. Cgs = 20 fF, Cgd = 5 fF and Cdb = 5 fF. Also, let µCox = 387 µA/V2, µpcox = 86 µ/V2, V’An = 5 V/µm, | V'Ap |= 6 V/µm. The bias current I= 0.2 mA and the bias current source has an output resistance Rss = 25 kW and an output capacitance Css = 0.2 pF. In addition to the capacitances introduced by the transistors at the output node, there is a capacitance Cx of 25 fF. It is required to determine the low-frequency values of Ad, Acm and CMRR. It is also required to find the poles and zero of Ad and the dominant pole of CMRR.
Solution
Since I = 0.2 mA. each of the four transistors is operating at a bias current of 100 µA. Thus, for Q1 and Q2,
The low-frequency value of the common-mode gain can be determined from Eq. (8.153) as
To determine the poles and zero of Ad we first compute the values of the two pertinent capac-itances Cm and CL. Using Eq. above,
Thus the dominant pole is that produced by CL at the output node. As expected, the pole and zero of the mirror are at much higher frequencies.
The dominant pole of the CMRR is at the location of the common-mode-gain zero introduced by Css and Rss, that is,
Thus, the CMRR begins to decrease at 31.8 MHz, which is much lower than fP1
MULTISTAGE AMPLIFIERS
Practical transistor amplifiers usually consist of a number of stages connected in cascade. In addition to providing gain, the first (or input) stage is usually required to provide a high input resistance in order to avoid loss of signal level when the amplifier is fed from a high-resistance source. In a differential amplifier the input stage must also provide large common-mode rejection. The function of the middle stages of an amplifier cascade is to provide the bulk of the voltage gain. In addition, the middle stages provide such other functions as the conversion of the signal from differential mode to single-ended mode (unless, of course, the amplifier output also is differential) and the shifting of the dc level of the signal in order to allow the output signal to swing both positive and negative.
Finally, the main function of the last (or output) stage of an amplifier is to provide a low output resistance in order to avoid loss of gain when a low-valued load resistance is con- nected to the amplifier. Also, the output stage should be able to supply the current required by the load in an efficient manner—that is, without dissipating an unduly large amount of power in the output transistors. We have already studied one type of amplifier configuration suitable for implementing output stages, namely, the source follower and the emitter follower. It can be shown that the source and emitter followers are not optimum from the point of view of power efficiency and so, more appropriate circuit configurations exist for output stages that are required to supply large amounts of output power.
To illustrate the circuit structure and the method of analysis of multistage amplifiers, we need to study two examples: a two-stage CMOS op amp and a four-stage bipolar op amp.
A Two-Stage CMOS Op Amp
Figure 36 shows a popular structure for CMOS op amps known as the two-stage configuration. The circuit utilizes two power supplies, which can range from ±2.5 V for the 0.5µm technology down to +0.9 V for the 0.18-µm technology. A reference bias current
FIGURE 8.436 Two-stage CMOS op-amp configuration
IREF is generated either externally or using on-chip circuits. One such circuit will be discussed shortly. The cur-rent mirror formed by Q8 and Q5 supplies the differential pair Q1 - Q2 with bias current.
The W/L ratio of Q5 is selected to yield the desired value for the input-stage bias current I (or I/2 for each of Q1 and Q2). The input differential pair is actively loaded with the current mirror formed by Q3 and Q4. The second stage consists of Q6, which is a common-source amplifier actively loaded with the current-source transistor Q8. A capacitor Cc is included in the negative-feedback path of the second stage. Its function is to enhance the Miller effect already present in Q6 (through the action of its Cgd) and thus provide the op amp with a dominant pole. By the careful placement of this pole, the op amp can be made to have a gain that decreases with frequency at the rate of -6 dB/octave, or, equivalently, -20 dB/decade down to unity gain or 0 dB. Op amps with such a gain function are guaranteed to operate in a stable fashion, as opposed to oscillating, with nearly all possible feedback connections. Such op amps are said to be frequency compensated. Here, we will simply take Cc into account in the analysis of the frequency response of the circuit in Fig.36.
A striking feature of the circuit in Fig. 36 is that it does not have a low-output-resistance stage. In fact, the output resistance of the circuit is equal to (r06 || ro7) and is thus rather high. This circuit, therefore, is not suitable for driving low-impedance loads. Never-theless, the circuit is very popular, and is used frequently for implementing op amps in VLSI circuits where the op amp needs to drive only a small capacitive load, for example, in switched- capacitor circuits. The simplicity of the circuit results in an op amp of reasonably good quality realized in a very small chip area.
Voltage Gain The voltage gain of the first stage was found in earlier to be given by
where gm1 is the transconductance of each of the transistors of the first stage, that is, Q1 and Q2. The second stage is an actively loaded common-source amplifier whose low-frequency voltage gain is given by
The dc open-loop gain of the op amp is the product of A1 and A2.
EXAMPLE
Consider the circuit in Fig.36 with the following device geometries (in µm).
Let IREF = 90 µA. Vtn = 0.7 V,Vtp = -0.8 V, µnCox = 160 µA/V2, µpCox = 40 µA/V2, | VA|(for all devices) = 10 V, VDD = Vss = 2.5 V. For all devices evaluate ID, |V0v|, |VGS|, gm, and ro Also find A1, A2, the dc open-loop voltage gain, the input common-mode range, and the output voltage range. Neglect the effect of VA on bias current.
Solution
Refer to Fig. 36. Since Q8 and Q5 are matched, I = IREF- Thus Q1, Q2. Q3. and Q4 each conducts a current equal to I/2 = 45 µA. Since Q7 is matched to Q5 and Q8, the current in Q7 is equal to IREF = 90µA. Finally, Q6 conducts an equal current of 90 µA. With ID of each device known, we use
to determine |Vov|for each transistor. Then we find |VGS| from | VGS| = |Vov|+|Vt| are given in Table below.
The transconductance of each device is determined from
The lower limit of the input common-mode range is the value of input voltage at which Q1 and Q2 leave the saturation region. This occurs when the input voltage falls below the voltage at the drain of Q1 by |Vtp| volts. Since the drain of Q1 is at-2.5 + 1 =-1.5 V. then the lower limit of the input common-mode range is -2.3 V.
The upper limit of the input common-mode range is the value of input voltage at which Q5 leaves the saturation region. Since for Q5 to operate in saturation the voltage across it (i.e., VSD5) should at least be equal to the overdrive voltage at which it is operating (i.e., 0.3 V), the highest volt-age permitted at the drain of Q5 should be +2.2 V. It follows that the highest value of vICM should be
V1CMmax = 2.2 -1.1 = 1.1V
The highest allowable output voltage is the value at which Q7 leaves the saturation region, which is VDD -| Vov7| = 2.5 - 0-3 = 2.2 V. The lowest allowable output voltage is the value at which Q6 leaves saturation, which is -VSS + Vov6 = -2.5 + 0.3 = -2.2 V. Thus, the output voltage range is – 2.2V to + 2.2V.
Input Offset Voltage The device mismatches present in the input stage give rise to an input offset voltage. The components of this input offset voltage can be calcu-lated using the methods developed earlier. Because device mismatches are random, the resulting offset voltage is referred to as random offset. This is to distinguish it from another type of input offset voltage that can be present even if all appropriate devices are perfectly matched. This predictable or systematic offset can be minimized by careful design.
To see how systematic offset can occur in the circuit of Fig. 36, let the two input terminals be grounded. If the input stage is perfectly balanced, then the voltage appearing at the drain of Q4 will be equal to that at the drain of Q3, which is (-Vss + VGS4). Now this is also the voltage that is fed to the gate of Q6. In other words, a voltage equal to VGS4 between gate and source of Q6. Thus the drain current of Q6, I6,will be related to the current of Q4, which is equal to I/2, by the relationship
In order for no offset voltage to appear at the output, this current must be exactly equal to the current supplied by Q7. The latter current is related to the current I of the parallel transistor Q5 by
If this condition is not met, a systematic offset will result. From the specification of the device geometries in above Example, we can verify that condition (185) is satisfied, and. therefore, the op amp analyzed in that example should not exhibit a systematic input offset voltage.
Frequency Response To determine the frequency response of the two-stage CMOS op amp of Fig. 36, consider its simplified small-signal equivalent circuit shown in Fig. 37. Here Gm1 is the transconductance of the input stage (Gm1 = gm1 = gm2), R1 is the output resistance of the first stage (R1 = ro2IIro4), and C1 is the total capacitance at the interface between the first and second stages
Gm2 is the transconductance of the second stage (Gm2 = gm6). R2 is the output resistance of the second stage (R2 = r06 II ro7), and C2 is the total capacitance at the output node of the op amp
where CL is the load capacitance. Usually CL is…m…uch.. l(a1r8g7e)r than the transistor capacitances, with the result that C2 is much larger than C1. Finally, note that in the equivalent circuit of Fig. 37 we should have included Cgd6 in parallel with Cc. Usually, however, Cc>> Cgd6, Cgd6 is neglected.
To eliminate Vi2 and thus determine Vo in terms of Vid, we use Eq. (189) to express Vid in terms of Vi2 and substitute the result into Eq. (188). After manipula-tions we obtain the amplifier transfer function
First we note that for s = 0 (i.e.. dc), Eq. 190 gives Vo/Vid = (GmlRl)(Gm2R2), which is what we should have expected. Second, the transfer function in Eq. 190 indicates that the amplifier has a transmission zero at s = sz, which is determined from
Also, the amplifier has two poles that are the roots of the denominator polynomial of Eq. (190). If the frequencies of the two poles are denoted wP1 and wP2 then the denominator polynomial can be expressed as
We recognize the first term in the denominator as arising at the interface between the first and second stages. Here, R1, the output resistance of the first stage, is interacting with the total capac-itance at the interface. The latter is the sum of C1 and the Miller capacitance Cc( 1 + Gm2R2), which results from connecting Cc in the negative-feedback path of the second stage whose gain is Gm2R2- Now, since R1 and R2 are usually of comparable value, we see that the first term in the denominator will be much larger than the second and we can approximate wP1 as
A further approximation is possible because C1 is usually much smaller than the Miller capacitance and Gm2R2>1 thus
The frequency of the second, non dominant pole can be found by equating the coefficients of the s2 terms in the denominator of Eq. (190) and in Eq. (194) and substituting for wPI from Eq. (197). The result is
In order to provide the op amp with a uniform gain rolloff of -20 dB/decade down to 0 dB. the value of the compensation capacitor Cc is selected so that the resulting value of wP1 (Eq. 197) when multiplied by the dc gain (Gm1,RlGm2R2) results in a unity-gain frequency wt lower than wz and wp2. Specifically
A Bias Circuit That Stabilizes gm The circuit presented has the interesting and useful property of providing a bias current whose value is independent of both the supply voltage and the
MOSFET threshold voltage. Furthermore, the transconductances of the transistors biased by this circuit have values that are determined only by a single resistor and the device dimensions.
The bias circuit is shown in Fig. 38. It consists of two deliberately mismatched transis- tors. Ql2 and Ql3 with Ql2 usually about four times wider than Q13 (Steininger, 1990; Johns and Martin. 1997). A resistor RB is connected in series with the source of Ql2. Since, as will be shown, RB determines both the bias current IB and the transconductance gm12, its value should be accurate and stable; in most applications, RB would be an off-chip resistor. In order to minimize the channel-length modulation effect on Q12, a cascode transistor Ql0 and a matched diode-connected transistor Q11 to provide a bias voltage for Ql0, is included. Finally, a p-channel current mirror formed by a pair of matched devices, Q8 and Q9, repli- cates the current IB back to Q11 and Q13, as well as providing a bias line for Q5 and Q7 of the CMOS op-amp circuit of Fig38. The circuit operates as follows:
The current mirror (Q8, Q9) causes Q13, to conduct a cur-rent equal to that in Ql2, that is, IB Thus,
from which we observe that IB is determined by the dimensions of Q12 and the value of RB and by the ratio of the dimensions of Q12 and Q13. Furthermore, Eq. (204) can be rearranged to the form

√(ID(W/L)), each transistor biased by the circuit of Fig. 38; that is, each transistor whose bias current is derived from IB will have a gm value that is a multiple of gm12 Specifically, the ith n-channel MOSFET will have
Finally, it should be noted that the bias circuit of Fig. 38 employs positive feedback, and thus care should be exercised in its design to avoid unstable performance. Instability is avoided by making Q12 wider than Q13, as has already been pointed out.
A Bipolar Op Amp
The second example of multistage amplifiers is the four-stage bipolar op amp shown in Fig.39. The circuit consists of four stages. The input stage is differential-in, differential-out and consists of transistors Q1 and Q2, which are biased by current source Q3. The second stage is also a differential-input amplifier, but its output is taken single-endedly at the collector of Q5. This stage is formed by Q4 and Q5, which are biased by the current source Q6. Note that the conversion from differential to single-ended as performed by the second stage results in a loss of gain by a factor of 2. A more elaborate method for accom-plishing this conversion was studied earlier; it involves using a current mirror as an active load.
In addition to providing some voltage gain, the third stage, consisting of the pnp transis- tor Q7 provides the essential function of shifting the dc level of the signal. Thus while the signal at the collector of Q5 is not allowed to swing below the voltage at the base of Q5 (+10 V), the signal at the collector of Q7 can swing negatively (and positively, of course). From our study of op amps we know that the output terminal of the op amp should be capable of both positive and negative voltage swings. Therefore every op-amp circuit in-cludes a level- shifting arrangement. Although the use of the complementary pnp transistor
provides a simple solution to the level-shifting problem, other forms of level shifter exist. Furthermore, level-shifting is accomplished in the CMOS op amp we have been studying by using complementary devices for the two stages: that is. p-channel for the first stage and n-channel for the second stage.
The output stage of the op amp consists of emitter follower Q8. As we know from our study of op amps, the output operates ideally around zero volts.





























Comments
Post a Comment