Integrated-circuit amplifiers part2.
The Basic MOSFET Current Source
Figure 5 shows the circuit of a simple MOS constant-current source. The heart of the circuit is transistor Q1 the drain of which is shorted to its gate, thereby forcing it to operate in the saturation mode with
where channel-length modulation is neglected. The drain current of Q1 is supplied by VDD through resistor R, which in most cases would be outside the IC chip. Since the gate currents are zero,
where the current through R is considered to be the reference current of the current source and is denoted IREF. Equations (6) and (7) can be used to determine the value required for R.
FIGURE 5 Circuit for a basic MOSFET constant-current source.
Now consider transistor Q2: It has the same VGS as Q1; thus, if we assume that it is operating in saturation, its drain current, which is the output current lo of the current source, will be
where we have neglected channel-length modulation. the above two equations enable us to relate the output current Io to the reference current IRFF as follows:
This is a simple and attractive relationship: The special connection of Q1 and Q2 provides an output current I0 that is related to the reference current IREF by the ratio of the aspect ratios of the transistors. In other words, the relationship between Io and IREF is solely determined by the geometries of the transistors. In the special case of identical transistors, I0 =
IREF, and the circuit simply replicates or mirrors the reference current in the output terminal. This has given the circuit composed of Q1, and Q2 the name current mirror, a name that is used irrespective of the ratio of device dimensions.
Figure 6 depicts the current mirror circuit with the input reference current shown as being supplied by a current source for both simplicity and generality. The current gain or current transfer ratio of the current mirror is given by Eq. (8).
Effect of V0 on I0 In the description above for the operation of the current source of Fig. 6, we assumed Q2 to be operating in saturation. This is obviously essential if Q2 is to supply a
FIGURE 6 Basic MOSFET current mirror.
constant-current output. To ensure that Q2 is saturated, the circuit to which the drain of
Q2 is to be connected must establish a drain voltage Vo that satisfies the relationship
or. equivalently. in terms of the overdrive voltage Vov of Q1 and Q2,
In other words, the current source will operate properly with an output voltage VO as low as Vov, which is a few tenths of a volt.
Although thus far neglected, channel-length modulation can have a significant effect on the operation of the current source. Consider, for simplicity, the case of identical devices Q1 and Q2. The drain current of Q2, IO, will equal the current in Q1, IREF, at the value of V0 that causes the two devices to have the same VDS, that is, at V0 = VGS. As V0 is
increased above this value, I0 will increase according to the incremental output resistance ro2 of Q2. This is illustrated in Fig. 7, which shows I0 versus V0. Observe that since Q2 is operating at a constant VGS (determined by passing IREF through the matched device Q1), the curve in Fig. 7 is simply the iD-vDS characteristic curve of Q2 for VGS equal to the particular value VGS.
In summary, the current source of Fig. 5 and the current mirror of Fig. 6 have a finite (.13
output resistance R0,
where I0 is given by Eq. (8) and VA2 is the Early voltage of Q2. Also, recall that for a given process technology, VA is proportional to the transistor channel length; thus, to obtain high output-resistance values, current sources are usually designed using transistors with relatively long channels. Finally, note that we can express the current I0 as
Figure7: Output characteristic of the current source in Fig. 5 and the current mirror of Fig. 6 for the case Q2 is matched to Q1.
EXAMPLE
Given VDD = 3 V and using IREF = 100 µA. it is required to design the circuit of Fig. 5 to obtain an output current whose nominal value is 100 µA. Find R if (Q1 and Q2 are matched and have channel lengths of 1 µm,. channel widths of 10µm. V1 = 0.7 V, and k'n = 200 µA/V2. What is the lowest possible value of V0? Assuming that for this process technology the Early voltage V'A = 20 V/µm. Find the output resistance of the current source. Also, find the change in output current resulting from a +1-V change in V0.
Solution
The output current will be 100 µA at V0 = VGS = 1V. If V0 changes by +1 V. the corresponding change in I0 will be
MOS Current – Steering Circuits
Once a constant current is generated, it can be replicated to provide DC bias currents for the various amplifier stages in the IC. Current mirrors can obviously be used to implement this current – steering function. Figure 8 shows a simple current – steering circuit.
FIGURE 8 A current-steering circuit.
Here Q1 together with R determine the reference current IREF. Transistors Q1, Q2, and Q3
form a two-output current mirror,

where Vov1 is the overdrive voltage at which Q1, Q2, and Q3 are operating. In other words, the drains of Q2 and (Q3 will have to remain higher than - Vss by at least the overdrive voltage, which is usually a few tenths of a volt.
Continuing our discussion of the circuit in Fig. 8, we see that current I3 is fed to the input side of a current mirror formed by PMOS transistors Q4 and Qs. This mirror provides
Finally, an important point to note is that while Q2 pulls its current I2 from a load (not shown in Fig. 8), Q5 pushes its current I5 into a load (not shown in Fig. 8). Thus Q5 is appropriately called a current source, whereas Q2 should more properly be called a current sink. In an IC, both current sources and current sinks are usually needed.
BJT Circuits
The basic BJT current mirror is shown in Fig. 9. It works in a fashion very similar to that of the MOS mirror. However, there are two important differences: First, the nonzero base current of the BJT (or, equivalently, the finite β) causes an error in the current transfer ratio of the bipolar mirror. Second, the current transfer ratio is determined by the relative areas of the emitter-base junctions of Q1, and Q2.
Let us first consider the case when β is sufficiently high so that we can neglect the base currents. The reference current IRFF is passed through the diode-connected transistor Q1 and thus establishes a corresponding voltage VBE, which in turn is applied between base and emitter of Q2. Now, if Q2 is matched to Q1 or, more specifically, if the EBJ area of Q2 is the same as that of Q1 and thus Q2 has the same scale current Is as Q1, then the collector current of Q2 will be equal to that of Q1; that is,
For this to happen, however, Q2 must be operating in the active mode, which in turn is achieved so long as the collector voltage V0 is 0.3 V or so higher than that of the emitter.
To obtain a current transfer ratio other than unity, say m, we simply arrange that the area of the EBJ of Q2 is m times that of Q1. In this case,
Figure : 10 Analysis of the current mirror taking into account the finite β of the BJTs
In general, the current transfer ratio is given by
Alternatively, if the area ratio m is an integer, one can think of Q2 as equivalent to m transistors, each matched to Q1 and connected in parallel.
Next we consider the effect of finite transistor β on the current transfer ratio. The analysis for the case in which the current transfer ratio is nominally unity—that is, for the case in which Q2 is matched to Q1—is illustrated in Fig. 10. The key point here is that since Q1 and Q2 are matched and have the same VBE, their collector currents will be equal. The rest of the analysis is straightforward. A node equation at the collector of Q1 yields
Note that as β approaches ∞, IREF approaches the nominal value of unity. For typical values of β, however, the error in the current transfer ratio can be significant. For instance, β = 100 results in a 2% error in the current transfer ratio. Furthermore, the error due to the finite β increases as the nominal current transfer ratio is increased. It can be shown that for a mirror with a nominal current transfer ratio m—that is, one in which IS2=mIS1 the actual current transfer ratio is given by
In common with the MOS current mirror, the BJT mirror has a finite output resistance R0,
Where VA2 and ro2 are the Early voltage and the output resistance, respectively, of Q2 Thus even if we neglect the error due to finite β, the output current I0 will be at its nominal value only when Q2 has the same VCE as Q1, namely at V0 = VBE. As V0 is increased, I0 will correspondingly increase. Taking both the finite β and the finite R0 into account, we can express the output current of a BJT mirror with a nominal current transfer ratio m as
We may observe, the error term due to the Early effect reduces to zero for V0 = VBE.
EXERCISE
Consider a BJT current mirror with a nominal current transfer ratio of unity. Let the transistors have Is = 10-15 A, β = 100, and VA = 100 V. For IREF = 1 mA, find I0 when V0 = 5V. Also, find the output resistance.
Ans. 1.02 mA: 100 kW
A Simple Current Source Just in the same way as MOS, the basic BJT current mirror can be used to implement a simple current source, as shown in Fig. 11. Here the reference current is
Current Steering
The current-steering approach described for MOS circuits can be applied in the bipolar case, which can be used to generate bias currents for amplifier stages in an IC. As an example, consider the circuit shown in Fig. 12.
The diode-connected transistor Q1, resistor R, and the diode-connected transistor Q2,
generate the required Iref
We assume, for the sake of simplicity that all the transistors have high β and thus that the base currents are very much negligible. The Early effect is also neglected. The diode- connected transistor Q1 and Q3 form a current mirror. So, Q3 will supply a constant current I1 equal to IREF. Transistor Q3 can supply this current to any load as long as the voltage that develops at the collector does not exceed (Vcc-0.3V); If it exceeds, Q3 enters the saturation region.

To generate a dc current twice the value of IREF, TWO transistors, Q5 and Q6, each of which is matched to Q1, are connected in parallel, and the combination forms a mirror with Q1 . Thus I3 = 2IREF.
The parallel combination of Q5 and Q6 is equivalent to a transistor with an EBJ area double of Q1 which is actually done when this circuit is fabricated in IC form.
Q4 forms a mirror with Q2; so Q4 provides a constant current I2, which equals IREF. If Q3 sources its current to parts of the circuit whose voltage should not exceed Vcc - 0.3V. Q4 sinks its current from parts of the circuit whose voltage should not decrease below, –VEE + 0.3 V.
To generate a current three times IREF. Three transistors, Q7, Q8 and Q9 each of which is matched to Q2, are connected in parallel, and the combination is placed in a mirror arrangement with Q2. Again, in an IC implementation, Q7, Q8, and Q9 shall be replaced with a transistor having a EBJ area three times that of Q2.
GENERAL CONSIDERATIONS IN HIGH FREQUENCY RESPONSE OF AMPLIFIERS
The amplifier circuits that we shall be going through further are intended for fabrication using IC technology. Therefore they do not use bypass capacitors. Moreover, the various stages in an integrated-circuit cascade amplifier are directly coupled; that is, they do not employ
FIGURE 13 Frequency response of a direct-coupled (dc) amplifier.
large coupling capacitors, such as what we observe in discrete circuits. The frequency response of these direct-coupled or DC amplifiers have the general form shown in Fig. 13. It is clear that the gain remains constant at its midband value AM down to zero frequency (DC). That is, compared to the capacitively coupled amplifiers that use bypass capacitors, direct-coupled IC amplifiers do not suffer gain reduction at low frequencies. However, gain falls off at the high-frequency end due to the internal capacitances of the transistor. These capacitances represent the charge storage phenomena that take place inside the transistors and are included in the high-frequency device models.
The High-Frequency Gain Function
The amplifier gain, considering the effect of internal transistor capacitances, can be expressed as a function of the complex-frequency variable s in the general form
Where AM is the mid-band gain, which is equal to the low-frequency or dc gain. The value of AM can be determined by analysing the amplifier equivalent circuit by neglecting the effect of the transistor internal capacitances—that is, considering them to act as open circuits. When we consider these capacitances, the gain has the factor FH(s), which can be expressed as shown below, in terms of its poles and zeros, which are usually real
where wPl, wP2, . . . , wPn are positive numbers indicating the frequencies of the n real poles and wz1, wz2,.... wZn are positive, negative, or infinite numbers indicating the frequencies of the n real transmission zeros. It is clear that, when s approaches 0, FH(s) approach unity and the gain approaches AM.
The 3-dB Frequency, fH
The region of the high-frequency band which is close to the midband, is the region of interest for an amplifier designer. The designer needs to estimate—and if need be modify—the value of the upper 3-dB frequency fH (or wH = 2πfH). It should be known that in many cases the zeros are either at infinity or such high frequencies as to be of little significance to the determination of wH. If one of the poles, say wPl, is of much lower frequency than any of the other poles, then this pole will have the greatest effect on the value of the amplifier wH. It means that, this pole (referred as dominant pole) will dominate the high-frequency response of the amplifier. In those cases the function FH(s) can be approximated by
which is the transfer function of a first-order (or Single Time Constant) low-pass network. So, if a dominant pole exists, then the value of wH can be written as
The lowest-frequency pole which is at least two octaves (a factor of 4) away from the nearest pole or zero can be referred as a dominant pole.
If a dominant pole does not exist, the 3-dB frequency wH can be determined from a plot of |FH(jw)|. Alternatively, an approximate formula for wH can be derived as follows: Consider, for the sake of simplicity, the case of a circuit that has two poles and two zeros in the high-frequency band; and so,
Substituting s = jw and considering the square of magnitude results
By definition, at w = wH, |FH|2 = ; thus,

This relationship can be extended to any number of poles and zeros as
From the above equation we may note that, if one of the poles, say wp1 is dominant, then Eq.39 reduces to Eq.34.
EXAMPLE
The high-frequency response of an amplifier is characterized by the transfer function
Determine the 3-dB frequency approximately and exactly.
Solution The lowest-frequency pole is 104 rad/s and is two octaves lower than the second pole and a decade lower than the zero, we note that a dominant-pole situation almost exists and wH = 104 rad/s. An estimate of wH can be determined using Eq.39, as follows:
The exact value of wH can be obtained from the given transfer function as 9537 rad/s., Fig. 14, represents a Bode and an exact plot for the given transfer function. This is a plot of the high-frequency response of the amplifier normalized relative to its midband gain.
Figure14: Normalized high- frequency response of the amplifier in Example.
Open-Circuit Time Constants
It is very clear that if the poles and zeros are known, then any one of the above methods can be used to find fH. Usually, it is not an easy task to find poles and zeros by hand analysis. In those cases, the following method is used which gives approximate value of fH.
The numerator and denominator factors of FH(s) (eq.32) can be multiplied out and FH(s) can be expressed in the form as shown below:
the coefficients b and a are related to the frequencies of the poles and zeros, respectively. The coefficient b1 can be written as,
The value of b1 can be obtained by considering the various capacitances in the high- frequency equivalent circuit one at a time while all other capacitors are set to zero (replacing them with open circuits) [see Gray and Searle (1969)]
This means, the value of b1 is obtained by adding the individual time constants, called
open-circuit time constants.
A capacitance Ci is considered, we reduce all other capacitances to zero, the input signal source is set to zero, and we find the resistance Rio as seen by Ci . This process is then repeated for all other capacitors in the circuit. Therefore, b1 is now given by,
[It is assumed that there are n capacitors in the high-frequency equivalent circuit]
The value of b1 obtained is exact. The approximation comes into picture when the value of b1 is used to determine wH. If the zeros are not dominant and if one of the poles, say P1, is dominant, then from Eq. (41), we may write,
Also, the upper cut-off (3-dB) frequency can be approximated as wP1, leading to
In the complicated circuits, it will be not known to us whether a dominant pole exists or not. However, we use the above equation to determine wH which gives good results in most of the cases.
EXAMPLE
Figure 15(a) shows the high-frequency equivalent circuit of a common-source MOSFET amplifier. The amplifier is fed with a signal generator Vsig having a resistance Rsig. Resistance Rin is due to the biasing network. Resistance R'L is the parallel equivalent of the load resistance RL, the drain bias resistance RD, and the FET output resistance r0. Capacitors Cgs and Cgd are the MOSFET internal capacitances. For Rsig = 100 kW, Rin
= 420 kΩ, Cgs = Cgd = 1pF, gm = 4 mA/V, and R'L =3.33 kW, find the midband voltage gain, AM= V0/Vsig and the upper 3-dB frequency, fH.
Solution
The midband voltage gain can be determined by considering the capacitors in the MOSFET model to be open circuits. This results in the midband equivalent circuit shown in Fig. 15(b), from which we find
AM=Vo/Vsig= -Rin(gm RL’)/(Rin+Rsig) = -10.8 V/V
wH is found using the method of open-circuit time constants. The resistance Rgs as seen by Cgs is found by setting Cgd =0 and short-circuiting the signal generator Vsig. This results in the circuit of Fig. 15(c), from which we find that
The resistance Rgd as seen by Cgd is found by setting Cgs = 0 and short-circuiting Vsig. The result is the circuit in Fig. 15(d), to which we apply a test current Ix. Writing a node equation at G gives
The method of open-circuit time constants specifies the circuit designer, which of the various capacitances is significant in determining the amplifier frequency response.
In the above example we see that Cgd is the dominant capacitance in determining fH. We also note that, in effect to increase fH either we use a MOSFET with smaller Cgd or, for a given MOSFET, we reduce Rgd by using a smaller R' or R'L. If R' is fixed, then for a given MOSFET the only way to increase bandwidth is by reducing the load resistance. Unfortunately, this also decreases the midband gain. This is an example of the usual trade-off between gain and bandwidth.
Miller's Theorem
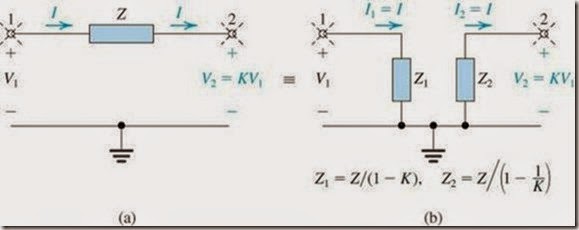
Consider the situation in Fig. 16(a), which can be a part of a larger circuit which is not shown. We observe two isolated circuit nodes, labeled 1 and 2, between which an impedance Z is connected. Nodes 1 and 2 are also connected to other parts of the circuit, as indicated by the dashed lines emanating from the two nodes. Furthermore, it is assumed that the voltage at node 2 is known and is related to that at node 1 by V2=KV1.
In typical situations K is a gain factor that can be +ve or -ve and has a magnitude usually larger than one.
FIGURE 16 The Miller equivalent circuit.
Miller's theorem states that impedance Z can be equivalently replaced by two impedances: Z1 connected between node 1 and ground and Z2 connected between node 2 and ground, where
to obtain the equivalent circuit shown in Fig. 16(b).
Proof of Miller's theorem can be given by deriving Eq. (45 &46) as follows:
In the original circuit of Fig. 16(a), from node-1 impedance Z carries the current I. Therefore, to keep this current unchanged in the equivalent circuit, we must choose the value of Z1 so that it draws an equal current.
which yields the value of Z1 in Eq. (45). Similarly, to keep the current into node 2 unchanged, we must choose the value of Z2 so that,

It should be known that the Miller equivalent circuit cannot be used directly to determine the output resistance of an amplifier. This is because in determining output resistances it is implicitly assumed that the source signal is reduced to zero and that a test-signal source is applied to the output terminals—leading to a major change in the circuit, which results Miller’s equivalent circuit to be invalid.
Example: Figure 17(a) shows an ideal voltage amplifier having a gain of -100 V/V with an impedance Z connected between its output and input terminals. Find the Miller equivalent circuit when Z is (a) a l-MW resistance, and (b) a 1-pF capacitance. Use the equivalent circuit to find Vo/Vsig
It is clear that Z1 is a capacitance of value 101C = 101 pF and Z2 is a capacitance 1.01 C
= 1.01 pF. The equivalent circuit is shown in Fig. 17(c), from which the voltage gain can be found as follows:
The transfer function of a first-order low-pass circuit with a dc gain of -100 and a cut-off frequency, f3dB
we see that the replacement of a feedback or bridging resistance results, for a negative K, in a smaller resistance [divided by a factor (1 - K)] at the input. If the feedback element is a capacitance, its value is multiplied by (1- K) to result in a equivalent capacitance at the input side. The multiplication of a feedback capacitance by (1 - K) is referred to as Miller’s multiplication or Miller’s effect.









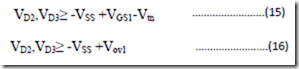
















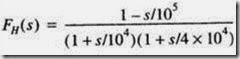


















Comments
Post a Comment