Integrated-circuit amplifiers (contd.) part2
The Common-Base Amplifier
Analysis of the common-base amplifier resembles that of the common-gate circuit that we analysed previously, with one major difference: The BJT has a finite β, and its base conducts signal current, which gives rise to the resistance rπ between base and emitter, looking into the base. Figure 17(a) shows the basic circuit for the active-loaded common- base amplifier without any details of biasing. Note that resistance RL represents the
Of load resistance, if any, and the output resistance of the current source that realizes the active load I.
Figure 17(b) shows the small-signal analysis performed directly on the circuit with the T model of the BJT used implicitly. The analysis is very similar to that for the MOS case except that, as a result of the finite base current, vi /rπ, the current io is related to ii by
which is the BJT counterpart of the MOS expression in Eq. (59). Another useful form for Rout can be obtained from (75),
which is the BJT counterpart of the MOS expression in Eq. (61). In Eq. (77) the second term is much larger than the first, resulting in the approximate expression
Equation (78) clearly shows that the inclusion of an emitter resistance Re increases the CB output resistance by a factor (1 + gmR'e). Thus, as Re is increased from 0 to ∞, the output resistance increases from ro to (1 +gmrπ)r0 = (1 + β)r0 = βr0. This upper limit on the value of Rout dictated by the finite β of the BJT, has no counterpart in the MOS case and will have important implications for circuit design. We note that for Re < rπ, Eq.
(78) can be approximated by
A useful summary of the formulas for Rin and Rout is provided in Fig. 19. The results above can be used to obtain the overall voltage gain Gv as
The high-frequency response of the common-base circuit can be evaluated in a manner similar to that used for the MOSFET.
EXERCISE
Consider the CB amplifier of Fig. 17(a) for the case I = 1 mA, β = 100, VA = 100 V, RL = 1 MW and Re = 1 kW. Find Rin, Avo, Ro, Av, Rout and Gv. Also find vo ,if vsig is a 5-mV peak sine wave.
Note:
The common-gate and common-base circuits have open-circuit voltage gains Avo almost equal to those of the common-source and common-emitter circuits.
Their input resistance, however, is much smaller and their output resistance much larger than the corresponding values for the CS and CE amplifiers. These two properties, though not usually desirable in voltage amplifiers, make the CG and CB circuits suitable as current buffers.
The absence of the Miller effect makes the high-frequency response of the CG and CB circuits far superior to that of the CS and CE amplifiers.
The most significant application of the CG and CB circuits is in a configuration known as the cascode amplifier, which we shall study next.
THE CASCODE AMPLIFIER
A common-gate (common-base) amplifier stage in cascade with a common source (common-emitter) amplifier stage, results in a very useful and versatile amplifier circuit known as the cascode configuration and has been in use in a wide variety of technologies for over three quarters of century.
The basic idea behind the cascode amplifier is to combine the high input resistance and large transconductance achieved in a common-source (common-emitter) amplifier with the current-buffering property and the superior high-frequency response of the common- gate (common-base) circuit. The cascode amplifier can be designed to obtain a wider bandwidth but equal dc gain as compared to the common-source (common-emitter) amplifier. Alternatively, it can be designed to increase the dc gain while leaving the gain- bandwidth product unchanged.
In many applications the cascade amplifier is thought of and treated as a single-stage amplifier though it is formed by cascading two amplifier stages.
The MOS Cascode
Figure 20(a) shows the MOS cascode amplifier. Here transistor Q1 is connected in the common-source configuration and provides its output to the input terminal (i.e., source) of transistor Q2. Transistor Q2 has a constant dc voltage, VB1AS, applied to its gate. Thus the signal voltage at the gate of Q2 is zero, and Q2 is operating as a CG amplifier with a constant-current load, I. Obviously both Q1 and Q2 will be operating at DC drain currents equal to I. As in previous cases, feedback in the overall circuit that incorporates the cascode amplifier establishes an appropriate dc voltage at the gate of Q1 so that its drain current is equal to I. Also, the value of VBIAS has to be chosen so that both Q1 and Q2 operate in the saturation region at all times.
Small-Signal Analysis : In response to the input signal voltage vi the common-source transistor Q1 conducts a current signal gm1vi, in its drain terminal and feeds it to the source terminal of the common-gate transistor Q2, called the cascode transistor. Transistor Q2 passes the signal current gm1vi on to its drain, where it is supplied to a load resistance RL (not shown in fig. 20) at a very high output resistance, Rout. The cascode transistor Q2 acts in effect as a buffer, presenting a low input resistance to the drain of Q1 and providing a high resistance at the amplifier output.
Characteristic parameters: In Fig. 20(b) shows the cascode circuit prepared for small- signal analysis and with a resistance RL shown at the output. RL is assumed to include the output resistance of current source I as well as an actual load resistance, if any. The diagram also indicates various input and output resistances obtained using the results of the analysis of the CS and CG amplifiers in previous sections. Note in particular that the CS transistor Q1 provides the cascode amplifier with an infinite input resistance. Also, at the drain of Q1 looking "downward”, see the output resistance of the CS transistor Q1, ro1. Looking "upward," we see the input resistance of the CG transistor Q2,
Figure 20 (b) also indicates that the output resistance of the cascode amplifier, Rout, is given by
This has been obtained using the formula in Eq. (59) and noting that the resistance Rs in the source of the CG transistor Q2 is the output resistance ro1 of Q1. Substituting for Avo2 from Eq. (83) into Eq.(85) yields.
Thus the cascode transistor increases the level of output resistance by a factor equal to its intrinsic gain, from ro1 of the CS amplifier to Aoro1.
From the cascode amplifier circuit in Fig. 20 (b), it is clear that when a signal source vsig with an internal resistance Rsig is connected to the input, the infinite input resistance of the amplifier causes.
The open circuit voltage gain Avo of the cascode amplifier can be easily determined from the circuit in Fig. 20(c), which shows the amplifier operating with the output open circuited. Since Rin2 will be infinite, the gain of the CS stage Q1 will be
The signal vo1 will be amplified by the open circuit voltage gain Avo2 of the CG transistor Q2 to obtain.
This confirms the value obtained earlier in the qualitative analysis.
The operation of the cascode amplifier is now clear: In response to vi the CS transistor provides a drain current gm1vi, which the CG transistor passes on to RL and, in the process, increases the output resistance by Ao. It is the increase in Rout to A0ro that increases the open-circuit voltage gain to (gm)(Aor0) = A2 .
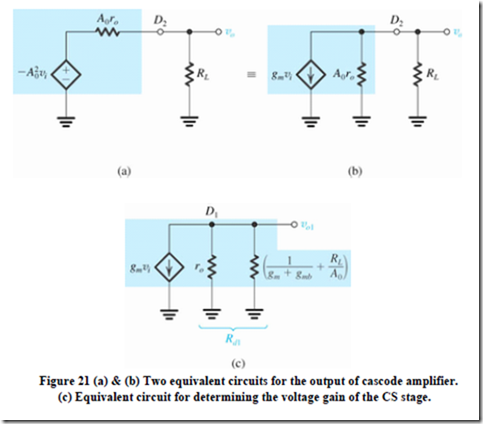
Figure 21 provides a useful summary of the operation: Two output equivalent circuits are shown in Fig. 21(a) and (b), and an equivalent circuit for determining the voltage gain of the CS stage Q1 is presented in Fig. 21(c). The voltage gain Av can be found from either of the two equivalent circuits in Fig. 21(a) and (b). From Fig. 21(a) we may write,
We see that if we are to realize the large gain of which the cascode is capable, resistance RL should be large. At the very least, RL should be of the order of A0ro. For
The gain of the CS stage is important because its value determines the Miller effect in that stage. From the equivalent circuit in Fig. 21(c), neglecting gmb,
Thus we see that when RL is large and the cascode amplifier is realizing a substantial gain, a good part of the gain is obtained in the CS stage. This is not good news considering the Miller effect, as we shall see shortly. To keep the gain of the CS stage relatively low. RL has to be lowered. For instance, for RL = ro, Eq. (94) indicates that
However, in this case the DC gain of the cascode is drastically reduced, as can be seen by substituting RL = ro in Eq. (92),
That is, the gain of the cascode becomes equal to that realized in a single CS stage. However, it does not mean that the cascode configuration (in this case) is not useful.
Frequency Response of the MOS Cascode
Figure 22 shows the cascode amplifier with all transistor internal capacitances indicated. Also included is a capacitance CL at the output node to represent the combination of Cdb2, the input capacitance of a succeeding amplifier stage (if any), and a load capacitance (if any). Cdb1 and Cgs2 appear in parallel, and we shall combine them in the following analysis. Similarly, CL and Cgd2 appear in parallel and will be combined.
The easiest and, in fact, quite insightful approach to determining the 3-dB frequency fH is to use the open-circuit time-constants method.
In the case of a large Rsig, the first term can dominate, especially if the Miller multiplier (1 +gm1Rd1) is large. This in turn happens when the load resistance RL is large (of the order of A0ro), causing Rin2 to be large and requiring the first stage, Q1 to provide a large proportion of the gain. It follows that when Rsig is large, to extend the bandwidth we have to lower RL to the order of r0. This in turn lowers Rin2 and hence Rdl and renders the Miller effect insignificant. However, the dc gain of the cascode will then be A0. Thus, while the dc gain will be the same as (or a little higher than) that achieved in a CS amplifier, the bandwidth will be greater.
In the case when Rsig is small, the Miller effect in Q1, will not be of concern. A large value of RL (on the order of A0ro) can then be used to realize the large dc gain possible with a cascode amplifier—that is, a dc gain on the order of A 2. Equation (98) indicates that in this case the third term will usually be dominant. To pursue this point a little further, consider the case Rsig = 0, and assume that the middle term is much smaller than the third term. It follows that
Which is of the same form as the formula for the CS amplifier with Rsig = 0. Here, however, (RL II Rout) is larger by a factor of about A0 compared to R’L in CS amplifier. Thus the fH of the cascode will be lower than that of the CS amplifier by the same factor A0. Figure 23 shows a sketch of the frequency response of the cascode and of the corresponding common-source amplifier. We observe that in this case cascoding increases the dc gain by a factor Ao while keeping the unity-gain frequency unchanged at
This example illustrates the advantages of cascoding by comparing the performance of a cascode amplifier with that of a CS amplifier in two cases:
a) The resistance of the signal source is significant, Rsig = 10 kW.
b) Rsig is negligibly small.
Thus cascoding increases the dc gain from 12.5 to 388 V/V. The unity-gain frequency (i.e., gain-bandwidth product), however, remains nearly constant.
The BJT Cascode
Figure 24(a) shows the BJT cascode amplifier. The circuit is very similar to the MOS cascode, and the small-signal analysis follows in a similar way, as shown in Fig. 24(b). The various input and output resistances have been shown. Unlike the MOSFET cascode, which has an infinite input resistance, the BJT cascode has an input resistance of rπ1 (neglecting rx). The formula for Rin2 is the one we found in the analysis of the common- base circuit. The output resistance Rout =β2ro2 found
FIGURE 24 (a) The BJT cascode amplifier, (b) The circuit prepared for small- signal analysis with various input and output resistances indicated. Note that rx is neglected, (c) The cascode with the output open-circuited.
by substituting Re2 = rol in Eq. (79) and making the approximation that gmro > β. Recall that βro is the largest output resistance that a CB transistor can provide.
The open-circuit voltage gain Avo and the no-load input resistance Ri can be found from the circuit in Fig. 24(c), in which the output is open-circuited. Observe that Rin2= rπ2 which is usually much smaller than r01. As a result the total resistance between the collector of Q1 and ground is approximately rπ2; thus the voltage gain realized in the CE transistor Q1 is –gm1rπ2 = -β. Recalling that the open-circuit voltage gain of a CB amplifier is (l + gmro) = Ao . We see that voltage gain Avo is
Putting all of these results together we obtain for the BJT cascode amplifier the equivalent circuit shown in Fig. 25(a). We note that compared to the common-emitter amplifier, cascoding increases both the open-circuit voltage gain and the output resistance by a factor equal to the transistor β. This should be contrasted with the factor A0 encountered in the MOS cascode. The equivalent circuit can be easily converted to the transconductance form shown in Fig.25(b). It shows that the short-circuit transconductance Gm of the cascode amplifier is equal to the transconductance gm of the BJTs. This should have been expected since Q1 provides a current gm1 vi to the emitter of the cascode transistor Q2, which in turn passes the current on (assuming α2 =1) to its collector and to the load resistance RL. In the process the cascode transistor raises the resistance level from ro at the collector of Q1 to βr0 at the collector of Q2. This is the by- now-familiar current-buffering action of the common-base transistor.
The voltage gain of the CE transistor Q1 can be determined from the equivalent circuit in fig-25(c). The resistance between the collector of Q1 and ground is the parallel equivalent
FIGURE : 25 (a) Equivalent circuit for the cascode amplifer in terms of the open – circuit voltage gain Avo = - βAo. (b) Equivalent circuit in terms of the overall short circuit transconductance Gm = gm . (c) Equivalent circuit for determining the gain of the CE stage Q1.
FIGURE 26: Determining the frequency response of the BJT cascode amplifier. Note that in addition to the BJT capacitances Cπ and Cµ the capacitance between the collector and the substrate Ccs for each transistor are also included.
of the output resistance of Q1, ro, and the input resistance of the CB transistor, Q2, namely Rin2 . Note that for RL < ro the latter reduces to re, as expected. However, Rin2 increases as RL is increased. Of particular interest is the value of Rin2 obtained for RL =βro, namely Rin2 = rπ/2. It follows that for this value of RL the CE stage has a voltage gain of -β/2.
Finally, in Fig. 26 the circuit and the formulas for determining the high-frequency response of the bipolar cascade are given. The analysis is similar to that studied in the MOSFET case.
A Cascode Current Source
We know that to realize the high voltage gain of which the cascode amplifier is capable the load resistance RL must be at least of the order of A0ro, for the MOSFET cascode or βro for the bipolar cascode. However, that RL includes the output resistance of the circuit which implements the current-source load I. This implies that the current-source must have output resistance that is at least Aor0 for the MOS case (βro for the BJT case). This means that the simple current-source circuits studied earlier cannot be considered, since their output resistances are equal to r0. Fortunately, there is a conceptually simple and

effective solution—namely, applying the cascoding principle to the current-source implementation. This is illustrated in Fig. 27, where Q1 is the current-source transistor and Q2 is the cascode transistor. VBlAS1 , is a DC voltage that is chosen so that Q1 provides the required value of I. VB1AS2 is chosen to keep Q2 and Q1, in saturation at all times. While the resistance looking into the drain of Q1 is rol, the cascode transistor Q2 multiplies this resistance by (gm2ro2) and provides an output resistance for the current source given approximately by
Similar arrangement can be used in the bipolar case also.
Double Cascoding
The essence of the operation of the MOS cascode is that the CG cascode transistor Q2 multiplies the resistance in its source, which is r0 of the CS transistor Q1, by its intrinsic gain A02 to provide an output resistance A02r01. It follows that we can increase the output resistance further by adding another level of cascoding, as shown in Fig. 28. Here another CG transistor Q3 is added, and this results in increased output resistance
by a factor Ao3 .Thus the output resistance of this double-cascode amplifier is A 2r . An additional bias voltage has to be generated for the additional cascode transistor Q3.
A drawback of double cascoding is that an additional transistor is now stacked between the power supply rails. Furthermore, since we are now dealing with output resistances on the order of A0ro, the current source I will also need to be implemented using a double cascode which adds yet one more transistor to the stack. It is appropriate to recall that in modern CMOS process technologies VDD is only a bit more than 1V.
Note that, since the largest output resistance possible in a bipolar cascode is βr0, adding another level of cascoding does not provide any advantage.
The Folded Cascode
To avoid the problem of stacking a large number of transistors across a low-voltage power supply, one can use a PMOS transistor for the cascode device, as shown in Fig.
29. Here as before, the NMOS transistor Q1 is operating in the CS configuration, but the CG stage is implemented using the PMOS transistor Q2. An additional current-source I2 is needed to bias Q2 and provide it with its active load. Note that Q1 is now operating at a bias current of (I1 – I2). Finally, a DC voltage VBIAS is needed to provide an appropriate dc level for the gate of the cascode transistor Q2. Its value has to be selected so that Q2 and Q1 operate in the saturation region.
The small-signal operation of the circuit in Fig. 29 is similar to that of the NMOS cascode. The difference here is that the signal current gmvi is folded down and made to flow into the source terminal of Q2, which gives the circuit the name folded cascode. The folded cascode is a very popular building block in CMOS amplifiers.
 FIGURE 29 The folded cascode
FIGURE 29 The folded cascode
BiCMOS Cascodes
The circuit designer can combine bipolar and MOS transistors in circuit configurations that take advantage of the unique features of each. As an example, Fig. 30 shows two possibilities for the BiCMOS implementation of the cascode amplifier. In the circuit of Fig. 30(a) a MOSFET is used for the input device, thus providing the cascode with an infinite input resistance. On the other hand, a bipolar transistor is used for the cascode device, thus providing a larger output resistance
than is possible with a MOSFET cascode. This is because β of the BJT is usually larger than Ao of the MOSFET and because ro of the BJT is much larger than r0 of modern submicron MOSFETs. Also, the bipolar CB transistor provides a lower input resistance Rin2 than is usually obtained with a CG transistor, especially when RL is low. The result is a lower total resistance between the drain of Q1 and ground and hence a reduced Miller effect in Q1.
The circuit in Fig. 30(b) utilizes a MOSFET to implement the second level of cascoding in a bipolar cascode amplifier. The need for a MOSFET stems from the fact that while the maximum possible output resistance obtained with a BJT is βro, there is no such limit with the MOSFET, and indeed, Q3 raises the output resistance by the factor A03.
THE CS AND CE AMPLIFIERS WITH SOURCE (EMITTER) DEGENERATION
Inserting a relatively small resistance (i.e. a small multiple of 1/gm) in the source of a CS amplifier (the emitter of a common-emitter amplifier) introduces negative feedback into the amplifier stage. As a result this resistance provides the circuit designer with an additional parameter that can be effectively utilized to obtain certain desirable properties as a trade-off for the gain reduction that source (emitter) degeneration causes.
The CS Amplifier with a Source Resistance
Figure 31(a) shows an active-loaded CS amplifier with a source resistance Rs. Note that a signal vbs will develop between body and source, and hence the body effect should be taken into account in the analysis. The circuit, prepared for small-signal analysis and with a resistance RL shown at the output, is presented in Fig. 31(b). To determine the output resistance Rout, we reduce vi, to zero, which makes the circuit identical to that of a CG amplifier. Therefore we can obtain Rout by using Eq. (58) as
The open-circuit voltage gain can be found from the circuit in Fig. 31(c). Noting that the current in Rs must be zero, the voltage at the source, vs, will be zero and thus vgs = vi and vbs = 0, resulting in
Utilizing Avo=-A0 and Rout from Eq. (105) gives us the amplifier output equivalent circuit shown in Fig. 31(d). An alternative equivalent circuit in terms of the short-circuit transconductance Gm is shown in Fig. 31(e), where Gm can be found from
Thus, if RL is kept unchanged, AV will decrease, which is the price paid for the performance improvements obtained when Rs is introduced. One such improvement is in the linearity of the amplifier. This comes about because only a fraction vgs of the input signal vi now appears between gate and source. Derivation of an expression for vgs/vi is significantly complicated by the inclusion of r0. The derivation should be done with the MOSFET equivalent-circuit model explicitly used. The result is
Thus the value of Rs can be used to control the magnitude of vgs so as to obtain the desired linearity—at the cost of gain reduction.
Frequency Response Another advantage of source degeneration is the ability to broaden the amplifier bandwidth. Figure 32(a) shows the amplifier with the internal capacitances Cgs and Cgd indicated. A capacitance CL that includes the MOSFET capacitance Cdb is also shown at the output. The method of open-circuit time constants can be employed to obtain an estimate of the 3-dB frequency fH. We observe in Fig. 32(b) the circuit for determining Rgd, which is the resistance seen by Cgd, We observe that Rgd can be determined by simply adapting the formula in Eq. (10) to the case with source
When Rsig is relatively large, the frequency response will be dominated by the Miller multiplication of Cgd. Another way for saying this is that CgdRgd will be the largest of the three open-circuit time constants that result in τH.
Now, as Rs is increased, the gain magnitude, |AM| = Gm R’L will decrease, causing Rgd to decrease (Eq.111), which in turn causes fH to increase (Eq.117). To highlight the trade-off between gain and bandwidth that Rs affords the designer, let us simplify the expression for Rgd in Eq. (111) by assuming that GmR’L > 1, and GmRsig>1
In practice, however, the other capacitances will play a role in determining fH, and ft will decrease somewhat as Rs is increased.
The CE Amplifier with an Emitter Resistance
Emitter degeneration is even more useful in the CE amplifier than source degeneration is in the CS amplifier. This is because emitter degeneration increases the input resistance of the CE amplifier. Figure 33 (a) shows an active-loaded CE amplifier with an emitter resistance Re usually in the range of 1 to 5 times re. Figure 33(b) shows the circuit for determining the
To determine the open-circuit voltage gain Avo, we utilize the circuit shown in Fig. 33(c). Analysis of this circuit is straightforward and can be shown to yield
That is, the open-circuit voltage gain obtained with a relatively small Re (i.e., of the order of re) remains very close to the value without Re.
The output resistance Ro is identical to the value of Rout that we derived for the CB circuit (Eq. 78),
The expressions for Rin, Avo ,and Ro in Eqs. (127), (128), and (130), respectively, can be used to determine the overall voltage gain for given values of source resistance and load resistance. Finally, we should mention that Avo and Ro can be used to find the effective short-circuit transconductance Gm ,of the emitter-degenerated CE amplifier as follows:

In summary, including a relatively small resistance Re (i.e.. a small multiple of re) in the emitter of the active-loaded CE amplifier reduces its effective transconductance by the factor ( 1 + gmRe) and increases its output resistance by the same factor, thus leaving the open-circuit voltage gain approximately unchanged. The input resistance Rin is increased by a factor that depends on Re and that is somewhat lower than ( 1 + gmRe). Also, including Re reduces the severity of the Miller effect and correspondingly increases the amplifier bandwidth. Finally, an emitter-degeneration resistance Re increases the linearity of the amplifier.








































Comments
Post a Comment