Differential Amplifiers and Multistage Amplifiers part2.
Common-Mode Gain and Common – Mode Rejection Ratio (CMRR)
We next consider the operation of the MOS differential pair when a common- mode input signal vicm is applied, as shown in Fig.10(a). Here vicm represents a disturbance or interfer-ence signal that is coupled to both input terminals. Although not shown, the dc voltage of the input terminals must still be defined by a voltage VCM as we have seen before. The symmetry of the circuit enables us to break it into two identical halves, as shown in Fig. 10(b). Each of the two halves, known as a CM half-circuit, is a MOSFET biased at I/2 and having a source degeneration resistance 2RSS. Neglecting the effect of r0,
we can express the voltage gain of each of the two identical half-circuits as
FIGURE 10 (a) The MOS differential amplifier with a common-mode input signal vicm (b) Equivalent circuit for determining the common-mode gain (with ro ignored). Each half of the circuit is known as the "common- mode half-circuit."
(b) The output is taken differentially:
Thus, even though Rss is finite, taking the output differentially results in an infinite CMRR. However, this is true only when the circuit is perfectly matched.
Effect of RD Mismatch on CMRR When the two drain resistances exhibit a mismatch of ΔRD as they inevitably do, the common-mode rejection ratio will be finite even if the output is taken differentially. To see how this comes about, consider the circuit in Fig. 10(b) for the case the load of Q1 is RD and that of Q2 is (RD + ΔRD). The drain signal voltages arising from vicm will be
In other words, the mismatch in RD causes the common-mode input signal vkm to be con-verted into a differential output signal: clearly an undesirable situation! Equation (8.49) indicates that the common-mode gain will be
Effect of gm Mismatch on CMRR Next the effect of a mismatch between the values of the transconductance gm of the two MOSFETs on the CMRR of the differential pair is considered. Since the circuit is no longer matched, we cannot employ the common-mode half-circuit. Rather, we refer to the circuit
Since Q1 and Q2 are in effect operating as source followers with a source resistance Rss that is typically much larger than 1/gm,
The similarity of this expression to that resulting from the RD mismatch (Eq.51) should be noted.
THE BJT DIFFERENTIAL PAIR
Fig12 shows the basic BJT differential-pair configuration. It is very similar to the MOSFET circuit and consists of two matched transistors, Q1 and Q2. whose emitters are joined together and biased by a constant-current source I. The latter is usually implemented by a current mirror transistor circuit. Although each collector is shown connected to the positive supply voltage
VCC through a resistance RC, this connection is not always seen—that is, in some applications the two collectors may be connected to other transistors rather than to resistive loads. It is necessary, that the collector circuits be such that Q1 and Q2 never enter saturation.
Basic Operation
To understand how the BJT differential pair works, consider first the case of the two bases joined together and connected to a common-mode voltage vCM,, as shown in Fig.13(a),
FIGURE12 The basic BJT differen-tial-pair configuration.
FIGURE13 Different modes of operation of the BJT differential pair:
(a) The differential pair with a common-mode input signal vCM (b) The differential pair with a "large" differential input signal (c) The dif-ferential pair with a large differential input signal of polarity opposite to that in (b)
(d) The differential pair with a small differential input signal vi. Note that we have assumed the bias current source I to be ideal (i.e.. it has an infinite output resistance) and thus I remains constant with the change in vCM.)
v = V B1 B2 =VCM. Since Q1 and Q2 are matched, and assuming an ideal bias current source I with infinite output resistance, it follows that the current I will remain constant and from symmetry that I will divide equally between the two devices. Thus iE1 = iE2 = I/2, and the voltage at the emitters will be (VCM - VBE) - where VBE is the base-emitter voltage (assumed in Fig13a to be approximately 0.7 V) corresponding to an emitter current of I/2. The voltage at each collector will be Vcc – (½)αIRc, and the difference in voltage between the two collectors will be zero.
Now let us vary the value of the common-mode input signal vCM. Obviously, as long as Q1 and Q2 remain in the active region the current I will still divide equally between Q1 and Q2, and the voltages at the collectors will not change. Thus the differential pair does not respond to (i.e., it rejects) common-mode input signals.
As another experiment, let the voltage vB2 be set to a constant value, say, zero (by grounding B2) and let vBl=+1 V (see Fig. 13b). It can be seen that Q1 will be on and conducting all of the current I and that Q2 will be off. For Q1 to be on (with VBE1 = 0.7 V), the emitter has to be at approximately +0.3 V, which keeps the EBJ of Q2 reverse-biased. The collector voltages will be vc1 = Vcc - αIRc and vc2 = Vcc.
Let us now change vB1 to -1 V (Fig.13c). Now it can be seen that Q1 will turn off, and Q2 will carry all the current I. The common emitter will be at -0.7 V, which means that the EBJ of Q1 will be reverse-biased by 0.3 V. The collector voltages will be vC1 = Vcc and vc2 = Vcc - αIRc.
From the foregoing, we see that the differential pair certainly responds to
large difference-mode (or differential) signals. In fact, with relatively small difference voltages we are able to steer the entire bias current from one side of the pair to the other. This current-steering property of the differential pair allows it to be used in logic circuits.
To use the BJT differential pair as a linear amplifier we apply a very small differential signal (a few millivolts), which will result in one of the transistors conducting a current of I/2 + DI; the current in the other transistor will be I/2
- DI, with DI being proportional to the difference input voltage (see Fig.13d). The output voltage taken between the two collectors will be 2αDIRc, which is proportional to the differential input signal vid.
Large-Signal Operation
We now present a general analysis of the BJT differential pair of Fig.12. If we denote the voltage at the common emitter by vE the exponential relationship applied to each of the two transistors may be written
The collector currents iC1 and ic2 can be obtained simply by multiplying the emitter currents in Eqs. (71) and (72) by α, which is normally very close to unity,
The fundamental operation of the differential amplifier is illustrated by Eqs.
(71) and (72). First,that the amplifier responds only to the difference voltage v,d. That is, if VB1 = VB2 = vCM, the current I divides equally between the two transistors irrespective of the value of the common-mode voltage vCM. This is the essence of differential-amplifier opera-tion, which also gives rise to its name.
Another important observation is that a relatively small difference voltage vid will cause the current I to flow almost entirely in one of the two transistors. Figure 14 shows a plot of the two collector currents (assuming α= 1) as a function of the differential input signal. This is a normalized plot that can be used universally. Note that a difference voltage of about 4VT (=100 mV) is
sufficient to switch the current almost entirely to one side of the BJT pair.
Note that this is much smaller than the corresponding voltage for the MOS pair,Ö2Vov. The fact that such a small signal can switch the current from one side of the BJT differential pair to the other means that the BJT differential pair can be used as a fast current switch. Another reason for the high speed of operation of the differential device as a switch is that neither of the transistors sat-urates.
The nonlinear transfer characteristics of the differential pair, shown in Fig.14. will not be utilized any further in this chapter. Rather, in the following we shall be interested specifically in the application of the differential pair as a small-signal amplifier. For this purpose the difference input signal is limited to less than about VT/2 in order that we may operate on a linear segment of the characteristics around the midpoint x (in Fig.14).
EXERCISE
For the BJT differential pair of Fig.12, find the value of input differential signal which is sufficient to cause iE1 = 0.99I
Ans. 115mV
Small-Signal Operation
In this section we shall study the application of the BJT differential pair in small-signal amplification. Fig.16 shows the BJT differential pair with a difference voltage signal vid applied between the two bases, implied is that the dc level at the input—that is, the common-mode input voltage—has been established. For instance, one of the two input terminals can be grounded and vid applied to the other input terminal. Alternatively, the differential amplifier may be fed from the output of another differential amplifier. In the latter case, the voltage at one of the input terminals will be VCM + vid /2 while that at the other input terminal will be VCM - vld/2. We will consider common-mode operation subsequently.
The Collector Currents When vid is Applied For the circuit of Fig.16, we may use Eqs. (71) and (72) to write
Equations (77) and (78) tell us that when vld = 0, the bias current I divides
equally between the two transistors of the pair. Thus each transistor is biased at an emitter current of I/2. When a "small-signal" vid is applied differentially (i.e., between the two bases), the col-lector current of Q1, increases by an increment ic and that of Q2 decreases by an equal amount. This ensures that the sum of the total currents in Q1 and Q2 remains constant, as constrained by the current-source bias. The incremental (or signal) current component ic is given by
Equation (78) has an easy interpretation. First, note from the symmetry of the circuit (Fig. 16) that the differential signal vid should divide equally between
the base-emitter junctions of the two transistors. Thus the total base-emitter voltages will be
where VBE is the DC BE voltage corresponding to an emitter current of I/2. Therefore, the collector current of Q1 will increase by gm vid/2 and the collector current of Q2 will decrease by gm vid/2. Here gm denotes the transconductance of Q1 and of Q2, which are equal and given by
………………… (82)
Differential Voltage Gain We have established that for small difference
input voltages (vid <2VT ; i.e.. vid smaller than about 20 mV) the collector currents are given by
The quantities in parentheses are simply the dc voltages at each of the two collectors.As in the MOS case, the output voltage signal of a bipolar differential amplifier can be taken either differentially (i.e., between the two collectors) or single-endedly (i.e., between one col-lector and ground). If the output is taken differentially, then the differential gain (as opposed to the common-mode gain) of the differential amplifier will be
On the other hand, if we take the output single-endedly (say, between the collector of Q1 and ground), then the differential gain will be given by
For the differential amplifier with resistances in the emitter leads (Fig.18) the differ-ential gain with the output is taken differentially is given by
This equation is a familiar one: It states that the voltage gain is equal to the ratio of the total resistance in the collector circuit (2RC) to the total resistance in the emitter circuit (2re + 2Re).
Equivalence of the Differential Amplifier to a Common-Emitter Amplifier The analysis and results on the previous page are quite similar to those obtained in the case of a common-emitter amplifier stage. That the
differential amplifier is in fact equivalent to a common-emitter amplifier is illustrated in Fig.19. Figure 19(a) shows a differential ampli-fier fed by a differential signal vid which is applied in a complementary (push-pull or balanced) manner. That is, while the base of Q1 is raised by vid/2, the base of Q2 is lowered by vid/2. We have also included the output resistance REE of the bias current source. From symmetry, it follows that the signal voltage at the emitters will be zero. Thus the circuit is equivalent to the two common- emitter amplifiers shown in Fig.19(b), where each of the two transistors is biased at an emitter current of I/2. Note that the finite output resistance REE of the current source will have no effect on the operation. The equivalent circuit in Fig.19(b) is valid for differential operation only.
In many applications the differential amplifier is not fed in a complementary fashion; rather, the input signal may be applied to one of the input terminals while the other terminal is grounded, as shown in Fig.20. In this case the signal voltage at the emitters will not be zero, and thus the resistance REE will have an effect on the operation. Nevertheless, if REE is large (REE > re), as is usually the case, then vld will still divide equally (approximately) between the two junctions, as shown in Fig.20. Thus the operation of the differential amplifier in this case will be almost identical to that in the case of symmetric feed, and the common-emitter equivalence can still be employed.
Since in Fig19 vc2 = -vcl, the two common-emitter transistors in Fig.19(b) yield similar results about the performance of the differential amplifier. Thus only one is needed to analyze the differential small-signal operation of the differential amplifier, and it is known as the differential half-circuit. If we take the common-emitter transistor fed with + vid/2 as the differential half- circuit and replace the transistor with its low-frequency equivalent
circuit model, the circuit in Fig.21 results. In evaluating the model parameters rπ.gm, and ro we must recall that the half-circuit is biased at I/2. The voltage gain of the differential amplifier (with the output taken differentially) is equal to the voltage gain of the half-circuit—that is. Vcl /(vld/2). Here, we note that including ro will modify the gain expression to
Common-Mode Gain and CMRR Fig.22(a) shows a differential amplifier fed by a common-mode voltage signal vicm. The resistance REE is the incremental output resistance of the bias current source. From symmetry we can say that the circuit is equivalent to that shown in Fig.22(b), where each of the two transistors Q1 and Q2 is biased at an emitter current I/2 and has a resistance 2REE in its emitter lead. Thus the common-mode output voltage vc1 will be
FIGURE 22 (a) The differential amplifier fed by a common-mode voltage signal vicm. (b) Equivalent "half-circuits" for common-mode calculations.
Now, if the output is taken differentially, then the output common-mode voltage v0 & (vc1 - vc2) will be zero and the common-mode gain also will be zero. On the other hand, if the output is taken single-endedly, the common mode gain Acm will be finite and given by
Each of the circuits in Fig.22(b) is called the common-mode half-circuit.
The analysis on the facing page assumes that the circuit is perfectly symmetrical. However, practical circuits are not perfectly symmetrical, with the result that the common-mode gain will not be zero even if the output is taken differentially. To illustrate, consider the case of perfect symmetry except for a mismatch ΔRC in the collector resistances. That is, let the collector of Q1 have a load resistance Rc. and Q2 have a load resistance Rc + ΔRC. It follows that
This expression can be rewritten as
Comparing with common-mode gain with that for single-ended output , we see that the common-mode gain is much smaller in the case of differential output. Therefore the input differential stage of an op amp, for example, is almost always a balanced one, with the output taken differentially. This ensures that the op amp will have the lowest possible common-mode gain or, equivalently, a high CMRR.
The input signals v1 and v2 to a differential amplifier usually contain a common-mode component, vicm,
FIGURE 24 Circuit for Example
(b) The voltage gain from the signal source to the bases of Q1 and Q2 is
The voltage gain from the bases to the output is
The overall differential voltage gain can now be found as
(c) Using Eq. (8.103).
where ΔRc= 0.02Rc in the worst case. Thus.
OTHER NONIDEAL CHARACTERISTICS OF THE DIFFERENTIAL AMPLIFIER
Input Offset Voltage of the MOS Differential Pair
Consider the basic MOS differential amplifier with both inputs grounded, as shown in Fig.25 (a). If the two sides of the differential pair were perfectly matched (i.e., Q1 and Q2 identical and RD1 = RD2 = RD) then current I would split equally between Q1 and Q2, and V0 would be zero. Practical circuits exhibit mismatches that result in a dc output voltage V0 even with both inputs grounded. We call V0 the output dc offset voltage. More commonly, we divide V0 by the differential gain of the amplifier, Ad, to obtain a quantity known as the input offset voltage, Vos,
Obviously, if we apply a voltage -Vos between the input terminals of the differential amplifier, then the output voltage will be reduced to zero (see Fig. 25b). This observation gives rise to the usual definition of the input offset voltage. It should be noted, however, that since the offset voltage is a result of device mismatches, its polarity is not known apriori.
Three factors contribute to the dc offset voltage of the MOS differential pair:
mismatch in load resistances, mismatch in W/L, and mismatch in Vt. We shall consider the three con-tributing factors one at a time,
For the differential pair shown in Fig.25(a) consider first the case where Q1 and Q2 are perfectly matched but RD1 and RD2 show a mismatch ΔRD; that is,
Because Q1 and Q2 are matched, the current I will split equally between them. Neverthe-less, because of the mismatch in load resistances, the output voltages VDI and VD2 will be
The corresponding input offset voltage is obtained by dividing V0 by the gain gmRD and sub-stituting for gm from Eq. (30). The result is
expressed us
Such a mismatch causes the current I to no longer divide equally between Q1 and Q2. Rather, it can be shown that the currents I1 and I2 will be
Input Offset Voltage of the Bipolar Differential Pair
The offset voltage of the bipolar differential pair shown in Fig.26(a) can be determined in a manner analogous to that used above for the MOS pair. Note, however, that in the bipolar case there is no analogous to the Vt mismatch of the MOSFET pair. Here the output offset results from mismatches in the load resistances Rc1 and Rc2 and from junction area. β, and other mismatches in Q1 and Q2. Consider first the effect of the load mismatch. Let
An important point to note is that in comparison to the corresponding expression for the MOS pair here the offset is proportional to VT rather than Vov/2. VT at 25 mV is 4 to 10 times lower than Vov/2. Hence bipolar differential pairs exhibit lower offsets than their MOS counterparts. As an example, consider the situation where the collector resistors are accurate to within ±1%. Then the worst case mismatch will be
Next consider the effect of mismatches in transistors Q1 and Q2. In particular, let the transistors have a mismatch in their emitter-base junction areas. Such an area mismatch gives rise to a proportional mismatch in the scale currents Is,
Refer to Fig.26(a) and note that VBEI = VBE2. Thus, the current I will split between Q1 and Q2 in proportion to their Is values, resulting in
As an example, an area mismatch of 4% gives rise to ΔIS/IS = 0.04 and an input offset voltage of 1 mV, Here again we note that the offset voltage is proportional to VT rather than to the much larger Vov. which determines the offset of the MOS pair due to Δ( W/L) mismatch.
THE DIFFERENTIAL AMPLIFIER WITH ACTIVE LOAD
As we have learnt earlier replacing the drain resistance RD with a constant- current source results in a much higher voltage gain as well as savings in chip area. The same, of course, applies to the differential amplifier. In this section we study a circuit for implementing an active-loaded differential amplifier and we shall study both the MOS and bipolar forms of this circuit.
The Active-Loaded MOS Differential Pair
Fig28(a) shows a MOS differential pair formed by transistors Q1 and Q2. loaded by a current mirror formed by transistors Q3 and Q4. To understand the operation consider first the quiescent state with the two input terminals connected to a dc voltage equal to the common-mode equilibrium value, in this case 0 V, as shown in Fig. 28(b). Assuming per-fect matching, the bias current I divides equally between Q1 and Q2. The drain current of Q1 , I/2, is fed to the input transistor of the mirror, Q3. Thus, a replica of this current is provided by the output transistor of the mirror, Q4. Observe that at the output node the two currents I/2 balance each other out, leaving a zero current to flow out to the next stage or to a load (not shown). If Q4 is perfectly matched to Q3, its drain voltage will track the voltage at the drain
FIGURE 28 (a) The active-loaded MOS differential pair, (b) The circuit at equilibrium assuming perfect matching, (c) The circuit with a differential input signal applied, neglecting the ro of all transistors.
of Q3; thus in equilibrium the voltage at the output will be VDD - VSG3. However, that in practical implementations, there will always be mismatches, resulting in a net dc current at the output. In the absence of a load resistance, this current will flow into the output resistances of Q2 and Q4 and thus can cause a large deviation in the output voltage from the ideal value. Therefore, this circuit is always designed so that the dc bias voltage at the output node is defined by a feedback circuit rather than by simply relying on the matching of Q4 and Q3.
Next, consider the circuit with a differential input signal vid applied to the input, as shown in Fig.28(c). Since we are now- investigating the small- signal operation of the circuit, we have removed the dc supplies (including the current source I). Also, for now ignore ro of all transistors. As Fig.28(c) shows, a virtual ground will develop at the common-source terminal of Q1 and Q2. Transistor Q1 will conduct a drain signal current = gm1vid/2 and transistor Q2 will conduct an equal but opposite current i. The drain signal cur-rent i of Q1, is fed to the input of the Q3 – Q4 mirror, which responds by providing a replica in the drain of Q4. Now, at the output node we have two currents, each equal to i, which sum together to provide an output current 2i. It is this factor
of 2, which is a result of the current mirror action, that makes it possible to convert the signal to single-ended form (i.e.. between the output node and ground) with no loss of gain! If a load resistance is connected to the out-put node, the current 2i flows through it and thus determines the output voltage Vo, In the absence of a load resistance, the output voltage is determined by the output current 2i and the output resistance of the circuit, as we shall shortly see.
Differential Gain of the Active-Loaded MOS Pair
As we know the output resistance ro of the transistor plays a significant role in the operation of active-loaded amplifiers. Therefore, we shall now take ro into account and derive an expression for the differential gain v0/vjd of the active-loaded MOS differential pair. Unfortunately, because the circuit is not symmetrical we will not be able to use the differential half-circuit technique. Rather, we shall perform the derivation from first principles: We will first find the short-circuit transconductance Gm and the output resistance Ro. Then, the gain will be determined as GmRo.
Determining the Transconductance Gm Fig29(a) shows the circuit prepared for determining Gm. Note that we have short-circuited the output to ground in order to find Gm as io/vid. Although the original circuit is not perfectly symmetrical, when the output is shorted to ground, the circuit becomes almost symmetrical. This is because the voltage between the drain of Q1 and ground is very small. This in turn is due to the low resistance between that node and ground which is almost equal to 1/gm3. Thus, we can invoke symmetry and assume that a virtual ground will appear at the source of Q1 and Q2 and in this way obtain the equivalent circuit shown in Fig.29(b). Here we have replaced the diode-connected transistor Q3 by its equivalent resistance [(1/gm3)]//ro3]. The voltage vg3 that develops at the common-gate line of the mirror can be found as
which for the usual case of rol and r03 > (1/gm3)reduces to
Thus the short-circuit transconductance of the circuit is equal to gm of each of the two tran-sistors of the differential pair. Here we should note that in the absence of the current-mirror action, Gm would be equal to gm/2.
Determining the Output Resistance R0 Fig.30 shows the circuit for determining Ro. Observe that the current i that enters Q2 must exit at its source. It then enters Q1, exiting at the drain to feed the Q3 – Q4 mirror. Since for the diode-connected transistor Q3, 1/gm3 is much smaller than ro3, most of the current i will flow into the drain of Q3. The mirror responds by providing an equal current i in the drain of Q4. It now remains to determine the relationship between i and vx. From Fig.30 we see that
where Ro2 is the output resistance of Q2. Now, Q2 is a CG transistor and has in its source lead the input resistance of Q1. The latter is connected in the CG configuration with a small resistance in the drain (approximately equal to 1/ gm3), thus its input resistance is approximately l/gm1. We can now use Eq.that was derived in the case of CG amplifier, to determine Ro2 by substituting gmb = 0 and Rs = l/gm1 to obtain
Common-Mode Gain and CMRR
Although its output is single-ended, the active-loaded MOS differential amplifier has a low common-mode gain and, correspondingly, a high CMRR. Fig31(a) shows the circuit with vicm applied and with the power supplies eliminated except, of course, for the output resistance Rss of the bias-current source I. Although the circuit is not symmetrical and hence we cannot use the common-mode half-circuit, we can split Rss equally between Q1 and Q2 as shown in Fig.31(b). It can now be seen that each of Q1 and Q2 is a CS transistor with a large source degeneration resistance 2RSS. We can use the formulas derived in CS amplifier with source resistance to determine the currents i1 and i2 that result from the application of an input signal vicm. Alternatively, we observe that since 2Rss is usually much larger than 1/gm of each of Q1 and Q2, the signals at the source terminals will be approximately equal to vicm. Also, the effect of ro1 and ro2 can be shown to be negligible. Thus, we can write
where ro1 = ro2 = ro and gm1 = gm2 = gm. Ro1 will be much greater than the parallel resistance introduced by Q3 namely (ro3 // (1/gm3)). Similarly, Ro2 will be much greater than ro4. Thus, we can easily neglect Ro1 and Ro2 in finding the total resistance between each of the drain nodes and ground.
The current i1 is passed through ((1 /gm3) // ro3) and as a result produces a voltage vg3
Since Rss is usually large, at least equal to ro, Acm will be small. The common- mode rejection ratio (CMRR) is now given by
We observe that to obtain a large CMRR we select an implementation of the biasing current source I that features a high output resistance. Such circuits include the cascade current source and the Wilson current source studied in previous unit.
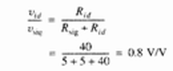
Comments
Post a Comment