Differential Amplifiers and Multistage Amplifiers part1

INRODUCTION

The most widely used building block in analog integrated-circuit design is the differential-pair or differential-amplifier configuration. For example, the input stage of every op-amp is a differential amplifier. Also, the BJT differential amplifier is the basis of a very-high-speed logic circuit family, called emitter-coupled logic (ECL).

It is the advent of integrated circuits that has made the differential pair extremely popular in both bipolar and MOS technologies. There are two reasons why differential amplifiers are so well suited for IC fabrication: First, the performance of the differential pair depends critically on the matching between the two sides of the circuit. Integrated- circuit fabrication is capable of providing matched devices whose parameters track over wide ranges of changes in environmental conditions. Second, differential amplifiers utilize more components (approaching twice as many) than single-ended cir-cuits. We may recall, that a significant advantage of integrated-circuit technology is the availability of large numbers of transistors at relatively low cost.

It is worthwhile to answer the question: Why differ-ential? Basically, there are two reasons for using differential in preference to single-ended amplifiers. First, differential circuits are much less sensitive to noise and interference than single-ended circuits. To elaborate this point, consider two wires carrying a small differential signal as the voltage difference between the two wires. Now, assume that there is an inter-ference signal that is coupled to the two wires, either capacitively or inductively. As the two wires are physically close together, the interference voltages on the two wires (i.e.. between each of the two wires and ground) should be equal. We know that, in a differential system, only the dif-ference signal between the two wires is sensed, and interference component will be absent.

The second reason for preferring differential amplifiers is that the differential configuration enables us to bias the amplifier and to couple amplifier stages together without the need for bypass and coupling capacitors. This is another reason why differential circuits are ideally suited for IC fabrication where large capacitors are impossible to fabricate economically.

This chapter covers the differential amplifier in both its MOS and bipolar implementations. It can be seen that the design and analysis of differential amplifiers makes extensive use of the stuff on single-stage amplifiers discussed earlier. The study of differential amplifiers follows with examples of multistage amplifiers, again in both MOS and bipolar technologies.

THE MOS DIFFERENTIAL PAIR

Fig. 1 shows the basic MOS differential-pair configuration, It consists of two matched transistors, Q1 and Q2, whose sources are joined together and biased by a constant-current source I. The latter is usually implemented by a MOSFET current mirror circuit. As of now, we assume that the current source is ideal and so it has infinite output resistance. Although each drain is shown connected

to the positive supply through a resistance RD in most cases active (current-source) loads are employed, as will be seen shortly. For the time being, to explain the essence of the differential-pair operation we utilize simple resistive loads. Whatever type of load is used, it is essential that the MOSFETs should always be operated in saturation.

Operation with a Common-Mode Input Voltage

To see how the differential pair works, consider first the case of the two gate terminals joined together and connected to a voltage vCM, called the common-mode voltage. That is, as shown in Fig.2, vG1 = vG2 = vCM. Since Q1 and Q2 are matched, it follows from symmetry that the current I will divide equally between the two transistors. Thus, iD1 = iD2 = I/2. and the voltage at the sources, vs , will be

where VGS is the gate-to-source voltage corresponding to a drain current of I/2. Neglecting channel-length modulation. VGS and I/2 are related by

Thus, the difference in voltage between the two drains will be zero.

Now, let us vary the value of the common-mode voltage VCM . Obviously, as long as Q1 and Q2 remain in the saturation region, the current I will divide equally between Q1 and Q2 and the voltages at the drains will not change. Thus the differential pair does not respond to (i.e.. it rejects) common-mode input signals.

An important specification of a differential amplifier is its input common-mode range. This is the range of vCM over which the differential pair operates properly. The highest value of VCM is limited by the requirement that Q1 and Q2 remain in saturation, thus

The lowest value of vCM, is determined by the need to allow for a sufficient voltage across cur-rent source I for it to operate properly. If a voltage Vcs is needed across the current source, then

Operation with a Differential Input Voltage

Now we apply a difference or differential input voltage by grounding the gate of Q2 (i.e.. setting vG2 = 0) and applying a signal vid to the gate of Q1, as shown in Fig. 4. It can be observed that since vid = vGS1 - vGS2, if vid is positive, vGS1 will be greater than vGS2 and hence iD1

 

will be greater than iD2 and the difference output voltage (vD2 - vD1) will be positive. On the other hand, when vid is negative, vGS1 will be lower than vGS2, and correspondingly vD1 will be higher than vD2; in other words, the difference or differential output voltage (vD2 - vD1) will be negative.

From the above, we see that the differential pair responds to difference-mode or differential input signals by providing a corresponding differential output signal between the two drains. At this point, it is useful to inquire about the value of vid that causes the entire bias current I to flow in one of the two transistors. In the positive direction, this happens when vGS1 reaches the value that corresponds to iD1 = I, and vGS2 is reduced to a value equal to the threshold voltage Vt at which point vs = -Vt. The value of vGS1 can be found from

where Vov is the overdrive voltage corresponding to a drain current of I/2 (Eq. 3), Thus, the value of Vid at which the entire bias current I is steered into Q1 is

which defines the range of differential-mode operation. It has been assumed that Q1 and Q2 remain in saturation even when one of them is conducting the entire current I.

To use the differential pair as a linear amplifier, we keep the differential input signal vld small. As a result, the current in one of the transistors (Q1 when vid is positive) will increase by an increment ΔI proportional to vid, to (I/2 + ΔI). Simultaneously, the current in the other transistor will decrease by the same amount to become (I/2 - ΔI). A voltage signal - ΔIRD develops at one of the drains and an opposite-polarity signal. ΔI RD, develops at the other drain. Thus the output voltage taken between the two drains will be 2ΔIRD, which is proportional to the differential input signal vid.

Large-Signal Operation

The expressions for the drain currents iD1 and iD2 in terms of the input differ-ential signal vid = vG1 – vG2. Since these expressions do not depend on the details of the circuit to which the drains are connected we do not observe these connections in Fig. 5; we simply assume that the circuit maintains Q1, and Q2 out of the triode region of operation at all times. The following derivation assumes that the differential pair is perfectly matched and neglects channel-length modulation (λ = 0) and the body effect.

To begin with, we express the drain currents of Q1 and Q2 as

Substituting for iD2 from Eq. (8.17) as iD2 = I - iD1 and squaring both sides of the resulting equation provides a quadratic equation in iD1 that can be solved to yield

Now since the increment in iD1 above the bias value of (I/2) must have the same polarity as vid. only the root with the "+" sign in the second term is physically meaningful; thus

The corresponding value of iD2 is found from iD2 = I – iD1

These two equations describe the effect of applying a differential input signal vjd on the currents iD1 and iD2. They can be used to obtain the normalized plots, iD1 /I and iD2/I versus vid/Vov, shown in Fig.6. Note that at vid = 0, the two currents are equal to I/2. Making Vid positive causes iDl to increase and iD2 to decrease by equal amounts so as to keep the sum constant, iD1 + iD2 = I. The current is steered entirely into Q1 when vid reaches the value Ö2Vov, as we found out earlier. For vid negative, identical statements can be made by inter- changing iD1 and iD2. In this case, vid = Ö2Vov steers the current entirely into Q2.

The transfer characteristics of Eqs. (23) and (24) and Fig. 6 are obviously non-linear. This is due to the term involving vid. Since we are interested in obtaining linear amplification from the differential pair, we will strive to make this term as small as possible. For a given

value of Vov. the only thing we can do is keep (vid/2) much smaller than Vov which is the condition for the small-signal approximation. It results in

which, as expected, indicate that iD1 increases by an increment id and iD2 decreases by the same amount, id. where id is proportional to the differential input signal vid.

Recalling from our study of the MOSFET that when it is biased at a current ID has a transconductance gm = 2ID/Vov, we recognize the factor (I/VoV) in Eq.

(27) as gm of each of Q1 and Q2, which are biased at ID = I/2. Now. why vid / 2? Simply because vid divides equally between the two devices with vgs1 = vid/ 2 and vgS2 = -vid/2, which causes Q1 to have a current increment id and Q2 to have a cur-rent decrement id.

Figure7 shows plots of the transfer characteristics iD1,2/I versus vid for various values of Vov, assuming that the current I is kept constant. These graphs clearly illustrate the linearity-transconductance trade-off obtained by changing the value of Vov: The linear range of oper-ation can be extended by operating

the MOSFETs at a higher Vov (by using smaller W/L ratios) at the expense of reducing gm and hence the gain. This trade-off is based on the assumption that the bias current I is kept constant. The bias current can, of course, be increased to obtain a higher gm. The expense for doing this, however, is increased power dis-sipation. a serious limitation in IC design.

SMALL-SIGNAL OPERATION OF THE MOS DIFFERENTIAL PAIR

In this section we consider the detailed operation of differential pair as a linear amplifier.

Differential Gain

Figure 8(a) shows the MOS differential amplifier with input voltages

Here, VCM denotes a common-mode dc voltage within the input common- mode range of the differential amplifier. It is needed in order to set the dc voltage of the MOSFET gates.

Typically VCM is at the middle value of the power supply. Thus, for our case, where two complementary supplies are utilized. VCM is typically 0 V.

The differential input signal vid is applied in a complementary (or balanced) manner; that is, vG1 is increased by vid/2 and vG2 is decreased by vid/

2. This would be the case, for instance, if the differential amplifier were fed from the output of another differential ampli-fier stage.

As indicated in Fig. 8(a) the amplifier output can be taken either between one of the drains and ground or between the two drains. In the first case, the resulting single-ended outputs vol and vo2 will be riding on top of the dc voltages at the drains ( VDD – I/2 RD). This is not the case when the output is taken between the two drains; the resulting differential output vo (having a 0 V dc component) will be entirely a signal component.

Our objective now is to analyze the small-signal operation of the differential amplifier of Fig. 8(a) to determine its voltage gain in response to the differential input signal vid. We observe in Fig. 8(b) the circuit with the power supplies removed and VCM eliminated. For the time being the effect of the MOSFET ro is neglected and also neglect the body effect (i.e., continue to assume that χ= 0). Finally each of Q1 and Q2 is biased at a dc current of I/2 and is operating at an overdrive voltage Vov.

From the symmetry of the circuit as well as because of the balanced manner in which vid is applied, we observe that the signal voltage at the joint source connection must be zero, acting as a sort of virtual ground. Thus Q1 has a gate-to-source voltage signal vgs1 = vid/2 and Q2 has vgs2 = -vid/2. Assuming vid/2 < Vov, the condition for the small-signal approximation, the changes resulting in the drain currents of Q1 and Q2 will be proportional to vgs1 and vgs2, respectively. Thus Q1 will have a drain current increment gm(vid/2) and Q2 will have a drain current decrement gm(vid/2), where gm denotes the equal transconductances of the two devices,

These results correspond to those obtained earlier using the large-signal transfer characteristics and imposing the small-signal condition, Eqs. (25) to (27).

It is useful at this point to observe again that a signal ground is established at the source terminals of the transistors without resorting to the use of a large bypass capacitor, clearly a major advantage of the differential-pair configuration.

The essence of differential-pair operation is that it provides complementary current signals in the drains; what we do with the resulting pair of complementary current signals is

a separate issue. Here, of course, we are simply passing the two current signals through a pair of matched resistors, RD, and thus obtaining the drain voltage signals

Alternatively, if the output is taken differentially, the gain becomes

Thus, another advantage of taking the output differentially is an increase in gain by a factor of 2 (6 dB).

An alternative and useful way of viewing the operation of the differential pair in response to a differential input signal vid is shown in Fig. 8(c). Here we are making use of the fact that the resistance between gate and source of a MOSFET. looking into the source, is 1/gm. As a result, between G1 and G2 we have a total resistance, in the source circuit, of 2/gm. It follows that we can obtain the current id simply by dividing vid by 2/gm as indicated in the figure.

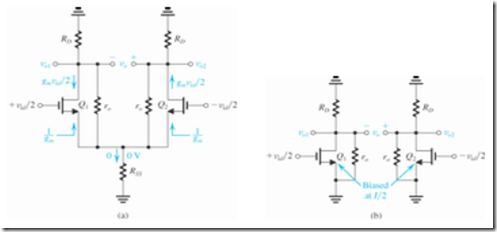
Effect of the MOSFET's ro Next we consider the effect of the finite output resistance ro of each of Q1 and Q2. As well, we make the realistic assumption that the bias current source I has a finite output resistance RSS. The resulting differential-pair circuit, prepared for small-signal analysis, is shown in Fig.9(a). Observe that the circuit remains perfectly symmetric, and as a result the voltage signal at the common source

FIGURE 9 (a) MOS differential amplifier with ro and Rss taken into account, (b) Equivalent circuil for determining the differential gain. Each of the two halves of the differential amplifier circuit is a common-source amplifier, known as its differential "half-circuit."

connection will be zero. Thus the signal current through Rss will be zero and Rss plays no role in determining the differential gain.

The virtual ground on the common source connection enables us to obtain the equivalent circuit shown in Fig. 9(b). It consists of two identical common- source amplifiers, one fed with +vid/2 and the other fed with -vid/2. Obviously we need only one of the two circuits to per-form any analysis we wish (including finding the frequency response, as we shall do shortly). Thus, either of the two common-source circuits is known as the differential half- circuit.

From the equivalent circuit in Fig. 9(b) we can write